
Trên cạnh \(BC\) của tam giác \(ABC\) lấy các điểm \(M,\,\,N,\) không trùng với \(B\) và \(C\) sao cho \(BM = MN = NC.\)
a) Chứng minh rằng hai tam giác \(ABC\) và \(AMN\) có cùng trọng tâm.
b) Gọi \(G\) là trọng tâm của tam giác \(ABC.\) Đặt \(\overrightarrow {GB} = \overrightarrow u \) và \(\overrightarrow {GC} = \overrightarrow v .\) hãy biểu thị các vectơ sau qua hai vectơ \(\overrightarrow u \) và \(\overrightarrow v :\,\,\overrightarrow {GA} ,\,\,\overrightarrow {GM} ,\,\,\overrightarrow {GN} .\)

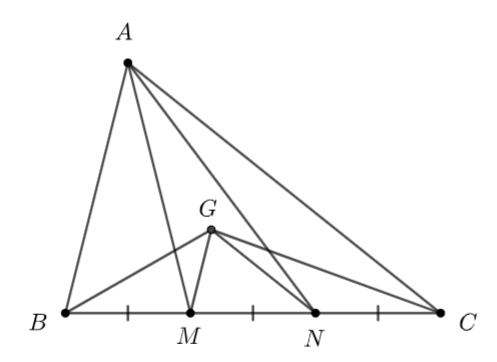
a) Ta có: \(\overrightarrow {AA} + \overrightarrow {BM} + \overrightarrow {CN} = \overrightarrow {BM} + \overrightarrow {CN} = \overrightarrow 0 \)
\( \Rightarrow \) hai tam giác \(ABC\) và \(AMN\) có cùng trọng tâm.
b) Gọi \(G\) là trọng tâm của tam giác \(ABC.\) Đặt \(\overrightarrow {GB} = \overrightarrow u \) và \(\overrightarrow {GC} = \overrightarrow v .\)
Advertisements (Quảng cáo)
Ta có: \(G\) là trọng tâm của tam giác \(ABC.\)
\( \Rightarrow \) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
\( \Rightarrow \) \(\overrightarrow {GA} = - \overrightarrow {GB} - \overrightarrow {GC} = - \overrightarrow u - \overrightarrow v = - \left( {\overrightarrow u + \overrightarrow v } \right)\)
Ta có: \(\overrightarrow {GM} = \overrightarrow {GB} + \overrightarrow {BM} \)
\( = \overrightarrow {GB} + \frac{1}{3}\overrightarrow {BC} \)
\(\begin{array}{l} = \overrightarrow {GB} + \frac{1}{3}\left( {\overrightarrow {GC} - \overrightarrow {GB} } \right)\\ = \frac{2}{3}\overrightarrow {GB} + \frac{1}{3}\overrightarrow {GC} = \frac{1}{3}\left( {2\overrightarrow u + \overrightarrow v } \right)\end{array}\)
Ta có: \(\overrightarrow {GN} = \overrightarrow {GC} + \overrightarrow {CN} \)
\(\begin{array}{l} = \overrightarrow {GC} + \frac{1}{3}\overrightarrow {CB} \\ = \overrightarrow {GC} + \frac{1}{3}\left( {\overrightarrow {GB} - \overrightarrow {GC} } \right)\\ = \frac{1}{3}\overrightarrow {GB} + \frac{2}{3}\overrightarrow {GC} = \frac{1}{3}\left( {\overrightarrow u + 2\overrightarrow v } \right)\end{array}\)
