
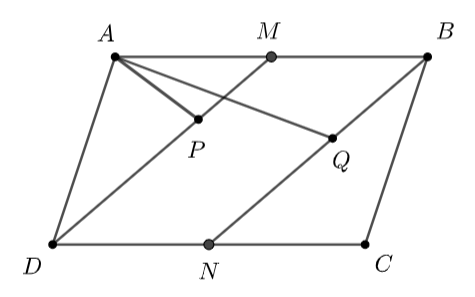
Cho hình bình hành \(ABCD.\) Gọi \(M,\,\,N\) theo thứ tự là trung điểm các cạnh \(AB,\,\,CD.\) Lấy \(P\) thuộc đoạn \(DM\) và \(Q\) thuộc đoạn \(BN\) sao cho \(DP = 2PM,\,\,BQ = xQN.\) Đặt \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AD} = \overrightarrow v .\)
a) Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\,\,\overrightarrow {AQ} \) qua hai vectơ \(\overrightarrow u \) và \(\overrightarrow v .\)
b) Tìm \(x\) để \(A,\,\,P,\,\,Q\) thẳng hàng.

a) Ta có: \(\overrightarrow {AP} = \overrightarrow {AD} + \overrightarrow {DP} \)
\(\begin{array}{l} = \overrightarrow {AD} + \frac{2}{3}\overrightarrow {DM} \\ = \overrightarrow {AD} + \frac{2}{3}\left( {\overrightarrow {AM} - \overrightarrow {AD} } \right) = \frac{1}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {AM} \\ = \frac{1}{3}\overrightarrow {AD} + \frac{2}{3}.\frac{1}{2}\overrightarrow {AB} = \frac{1}{3}\overrightarrow u + \frac{1}{3}\overrightarrow v \end{array}\)
Advertisements (Quảng cáo)
Ta có: \(BQ = xQN\)
\( \Rightarrow \) \(\overrightarrow {BQ} = x\overrightarrow {QN} \)
\( \Leftrightarrow \) \(\overrightarrow {AQ} - \overrightarrow {AB} = x\left( {\overrightarrow {AN} - \overrightarrow {AQ} } \right)\)
\(\begin{array}{l} \Leftrightarrow \,\,\left( {x + 1} \right)\overrightarrow {AQ} = \overrightarrow {AB} + x\overrightarrow {AN} \\ \Leftrightarrow \,\,\left( {x + 1} \right)\overrightarrow {AQ} = \overrightarrow {AB} + x\left( {\overrightarrow {AD} + \overrightarrow {DN} } \right) = x\overrightarrow {AD} + \overrightarrow {AB} + x.\frac{1}{2}\overrightarrow {AB} \\ \Leftrightarrow \,\,\left( {x + 1} \right)\overrightarrow {AQ} = x\overrightarrow {AD} + \left( {\frac{1}{2}x + 1} \right)\overrightarrow {AB} \\ \Leftrightarrow \,\,\left( {x + 1} \right)\overrightarrow {AQ} = x\overrightarrow v + \left( {\frac{1}{2}x + 1} \right)\overrightarrow u \\ \Leftrightarrow \,\,\overrightarrow {AQ} = \frac{{x + 2}}{{2\left( {x + 1} \right)}}\overrightarrow u + \frac{x}{{x + 1}}\overrightarrow v \end{array}\)
b) Để \(A,\,\,P,\,\,Q\) thẳng hàng
\( \Leftrightarrow \) \(\overrightarrow {AP} \) và \(\overrightarrow {AQ} \) cùng phương
\( \Leftrightarrow \,\,\frac{{x + 2}}{{2\left( {x + 1} \right)}}:\frac{1}{3} = \frac{x}{{x + 1}}:\frac{1}{3}\) (Điều kiện: \(x \ne - 1\))
\(\begin{array}{l} \Leftrightarrow \,\,\frac{{x + 2}}{2} = x\\ \Leftrightarrow \,\,2x = x + 2\end{array}\)
\( \Leftrightarrow \,\,x = 2\) (thỏa mãn)
Vậy \(x = 2\) thì \(A,\,\,P,\,\,Q\) thẳng hàng
