Với mỗi hàm số bậc hai cho dưới đây: \(y = f(x) = - {x^2} - x + 1\); \(y = g(x) = {x^2} - 8x + 8\)
Hãy thực hiện các yêu cầu sau:
a) Viết lại hàm số bậc hai dưới dạng \(y = a{(x - h)^2} + k\)
b) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số
c) Vẽ đồ thị của hàm số

a) Ta có:
\(y = f(x) = - {x^2} - x + 1 \Leftrightarrow f(x) = - \left( {{x^2} + x + \frac{1}{4}} \right) + \frac{5}{4} \Leftrightarrow f(x) = - {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4}\)
\(y = g(x) = {x^2} - 8x + 8 \Leftrightarrow g(x) = {x^2} - 8x + 16 - 8 \Leftrightarrow g(x) = {(x - 4)^2} - 8\)
Advertisements (Quảng cáo)
b) Ta có:
\(f(x) = - {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4} \le \frac{5}{4}\) \( \Rightarrow \) GTLN của f(x) là \(\frac{5}{4}\) đạt được khi \(x = - \frac{1}{2}\)
\(g(x) = {(x - 4)^2} - 8 \ge - 8 \Rightarrow \) GTNN của g(x) là -8 đạt được khi x = 4
c)
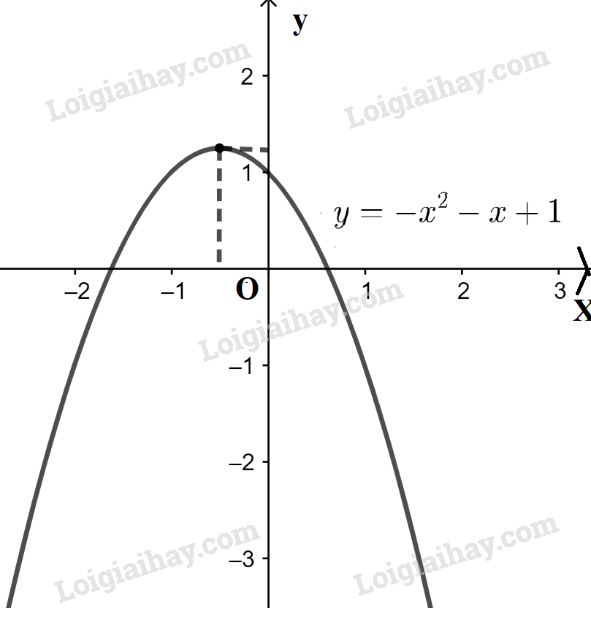
- Đồ thị hàm số \(y = - {x^2} - x + 1\) là đường parabol có a = -1 < 0 nên có bề lõm quay xuống dưới.
Đỉnh \(I\left( { - \frac{1}{2};\frac{5}{4}} \right)\), trục đối xứng x = \( - \frac{1}{2}\). Giao điểm của parabol với trục Oy là điểm (0 ; 1) và cắt trục Ox tại 2 điểm có hoành độ \(x = \frac{{ - 1 - \sqrt 5 }}{2}\) và \(x = \frac{{ - 1 + \sqrt 5 }}{2}\)
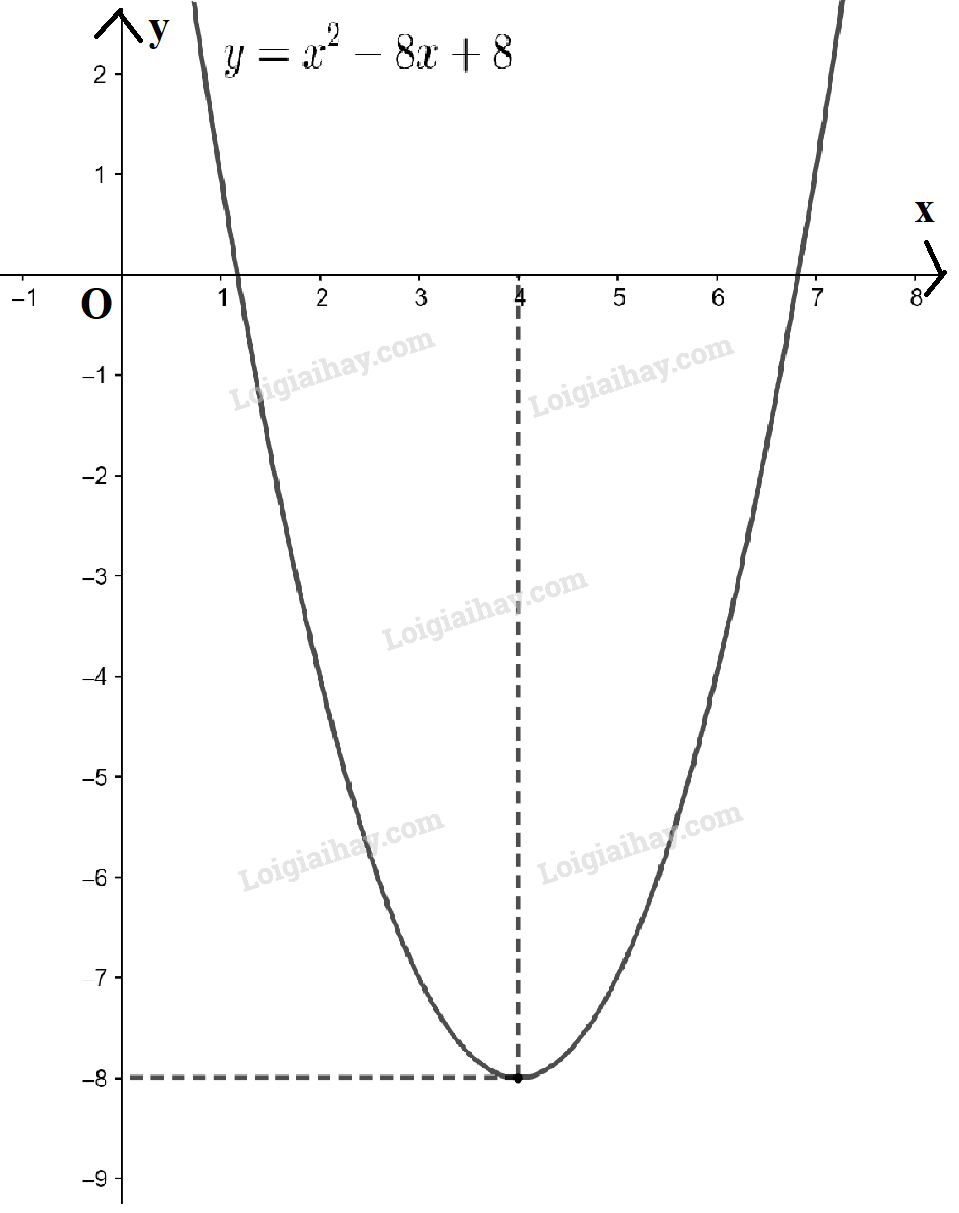
- Đồ thị hàm số \(y = {x^2} - 8x + 8\) là đường parabol có a = 1 > 0 nên có bề lõm quay lên trên
Đỉnh \(I(4; - 8)\), trục đối xứng x = 4. Giao điểm của parabol với trục Oy là điểm (0 ; 8) và cắt trục Ox tại 2 điểm có hoành độ \(x = 4 - 2\sqrt 2 \) và \(x = 4 + 2\sqrt 2 \)