Trong mặt phẳng Oxy cho đường thẳng \(\Delta 😡 - y + 2 = 0\) và điểm A(2;0).
a) Chứng mình rằng hai điểm A và O nằm về cùng một phía đối với đường thẳng .
b) Tìm điểm M trên \(\Delta \) sao cho độ dài đường gấp khúc OMA ngắn nhất.
Gợi ý làm bài
(h.3.11)
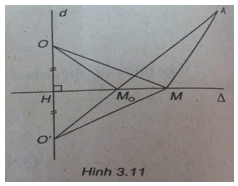
Ta có:
\(\Delta \left( O \right) = 2 > 0\)
\(\Delta \left( A \right) = 2 + 2 > 0\)
Vậy A và O nằm về cùng một phía đối với \(\Delta \)
b) Gọi O’ là điểm đối xứng của O qua \(\Delta \), ta có:
Advertisements (Quảng cáo)
\(OM + MA = O’M + MA \ge O’A\)
Ta có : OM + MA ngắn nhất
\( \Leftrightarrow O’,M,A\) thẳng hàng
Xét đường thẳng d đi qua O và vuông góc với \(\Delta \) . Phương trình của d là:
x + y = 0
d cắt \(\Delta \) tại H(-1;1).
H là trung điểm của OO’ suy ra \(O’\left( { - 2;2} \right)\)
Phương trình đường thẳng O’A là: x + 2y - 2 = 0
Giải hệ phương trình
\(\left\{ \matrix{
x + 2y = 2 \hfill \cr
x - y = - 2 \hfill \cr} \right.\)
ta được \(M = \left( { - {2 \over 3};{4 \over 3}} \right).\)
