
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} \)và \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều là 10 N và \(\widehat {AMB} = 90^\circ \) Tìm độ lớn của lực \(\overrightarrow {{F_3}} \).

Ba lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) cùng tác dụng vào M và vật đứng yên nên hợp lực của chúng có giá trị bằng không, hay: \(\)\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
Dựng hình bình hành \(MADB\), khi đó: \(\overrightarrow {MA} + \overrightarrow {MB}= \overrightarrow {MD}\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {MC} = \overrightarrow {0}\)
\( \Rightarrow \overrightarrow {MD}, \overrightarrow {MC}\) là hai vecto đối nhau
Advertisements (Quảng cáo)
\( \Rightarrow MD =MC\)
Như vậy ta đã xác định được phương, chiều của lực \(F_3\)
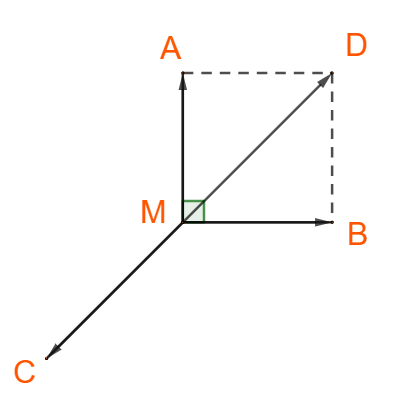
Xét hình bình hành MADB, ta có:
AM=AB và \(\widehat {AMB} = 90^\circ \)
\( \Rightarrow\) MADB là hình vuông, cạnh \(AB=10\)
\( \Rightarrow MC = MD = AB. \sqrt{2} = 10\sqrt{2}\)
Vậy độ lớn của lực \(\overrightarrow {{F_3}} \) là \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = MC = 10\sqrt 2 \) (N)
