
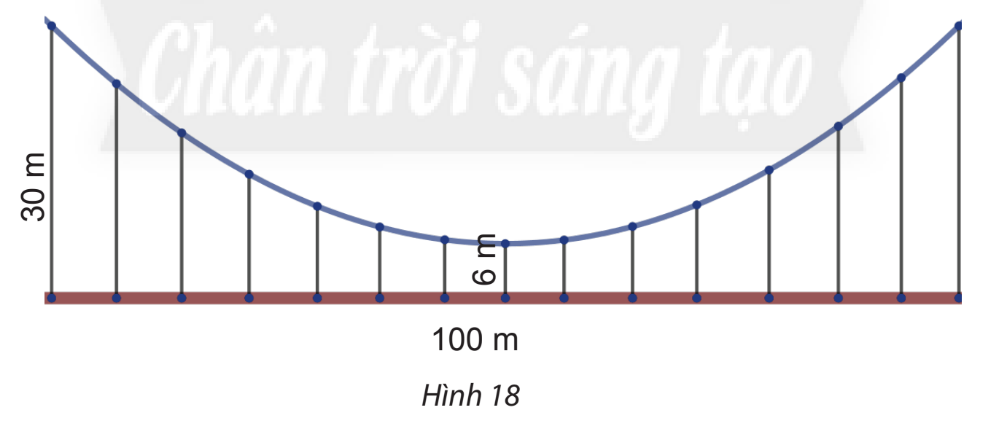
Một cái cầu có dây cáp treo như hình vẽ parabol, cầu dài 100 m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m

Bước 1: Gắn hệ trục tọa độ với gốc tọa độ tại điểm giữa cầu
Bước 2: Xác định phương trình mô tả hình dạng của cầu
Bước 3: Thay giả thiết vào phương trình vừa tìm được để tìm chiều dài thanh treo cầu
Advertisements (Quảng cáo)

Chọn hệ tọa độ Oxy với gốc tọa độ tại điểm trên của thanh ngắn giữa cầu, trục tung tương ứng là mặt đường của cầu, vẽ lại hình như dưới đây
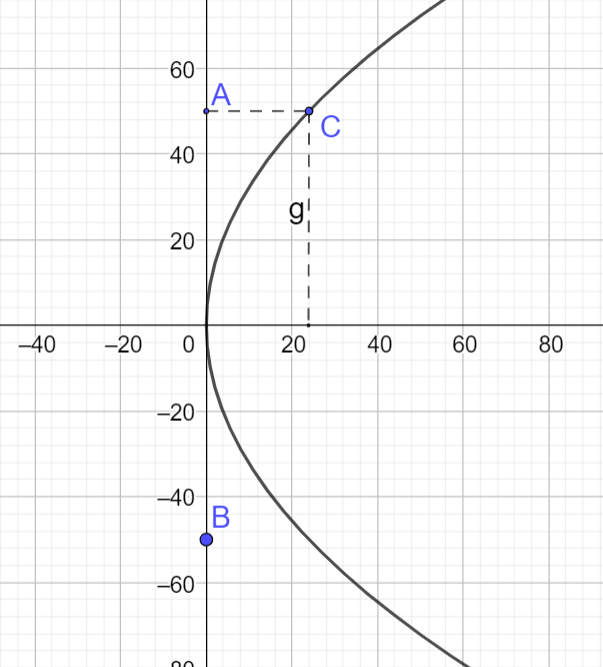
Ta nhận thấy cầu có dạng parabol nên gọi phương trình mô tả hình dạng cầu là \({y^2} = 2px\)
Cầu dài 100 m tương ứng \(AB = 2OB = 100 \Rightarrow OB = 50\), thanh dài nhất dài 30 m
Từ đó ta có tọa độ điểm \(C(24;50)\)
Thay tọa độ C vào phương trình \({y^2} = 2px\) ta có \(2500 = 2p.24 \Rightarrow p = \frac{{625}}{{12}}\)
Ta có phương trình mô tả cây cầu là \({y^2} = \frac{{625}}{6}x\)
Tại thanh cách điểm giữa cầu 18m thì \(x = 18\) ta có \({18^2} = \frac{{625}}{6}.x \Rightarrow x \approx 3,11\)
Vậy chiều dài của thanh cách điểm giữa cầu 18m gần bằng 3,11 m
