HĐ Khám phá 3
Lấy một tấm bìa, trên đó đánh dấu hai điểm \({F_1}\) và \({F_2}\). Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho \(d - l = 2a\) nhỏ hơn khoảng cách \({F_1}{F_2}\) (hình 6a).
Đính một đầu dây vào đầu A của thước, dùng đinh ghim đầu dây còn lại vào điểm \({F_2}\). Đặt thước sao cho đầu B của thước trùng với điểm \({F_1}\). Tựa đầu bút chì vào dây, di chuyển điểm M trên tấm bìa và giữ sao cho dây luôn căng, đoạn AM ép sát vào thước, khi đó M sẽ gạch lên tấm bìa một đường (H) (xem hình 6b)
a) Chứng tỏ rằng khi M di động, ta luôn có \(M{F_1} - M{F_2} = 2a\)
b) Vẫn đính một đầu dây vào đầu A của thước nhưng đổi chỗ cố định đầu dây còn lại vào \({F_1}\), đầu B của thước trùng với \({F_2}\) sao cho đoạn thẳng BA có thể quay quanh \({F_2}\)và làm tương tự như lần đầu để bút chì M vẽ được một nhánh khác của đường (H) (hình 6c). Tính \(M{F_2} - M{F_1}\)
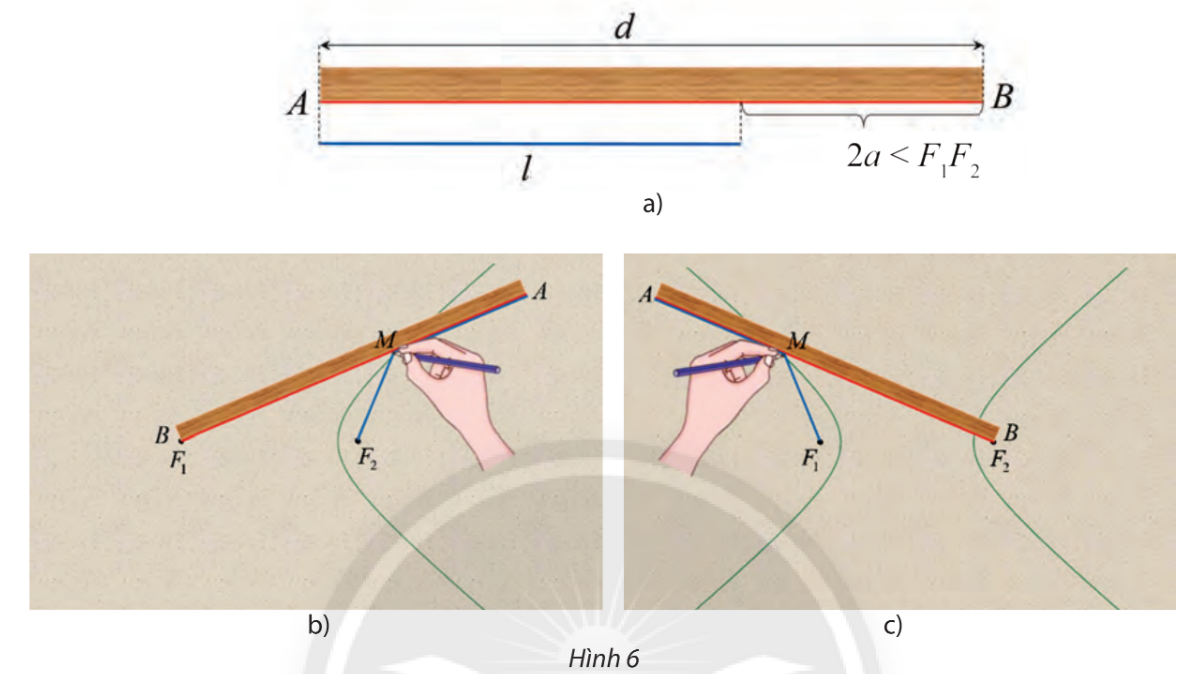

a) Khi điểm M trùng với điểm A ta có:
\(M{F_1} - M{F_2} = A{F_1} - A{F_2} = AB - A{F_2} = d - l = 2a\)
b) Tương tự khi điểm M trùng với điểm A ta có:
\(M{F_2} - M{F_1} = A{F_2} - A{F_1} = AB - A{F_1} = d - l = 2a\)
HĐ Khám phá 4
Cho hyperbol (H) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt điểm \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (H) \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)
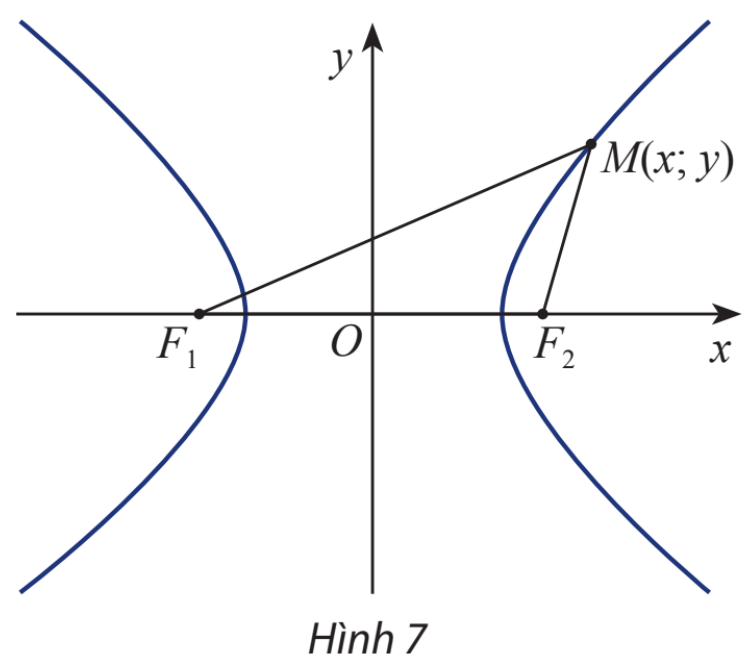

Sử dụng phương pháp tọa độ trong mặt phẳng

a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
Advertisements (Quảng cáo)
b) Ta có \(M(x;y) \in (E)\) nên \(\left| {{F_1}M - {F_2}M} \right| = 2a \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)
Thực hành 2
Viết phương trình chính tắc của hypebol có tiêu cự bằng 10 và độ dài trục nhỏ bằng 6.

Phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (H);b = \sqrt {{c^2} - {a^2}} \)

Ta có: \(2c = 10 \Rightarrow c = 5,2b = 6 \Rightarrow b = 3\)
Suy ra \(a = \sqrt {{c^2} - {b^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Vậy phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
Vận dụng 2
Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (hình 9). Cho biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tìm bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.
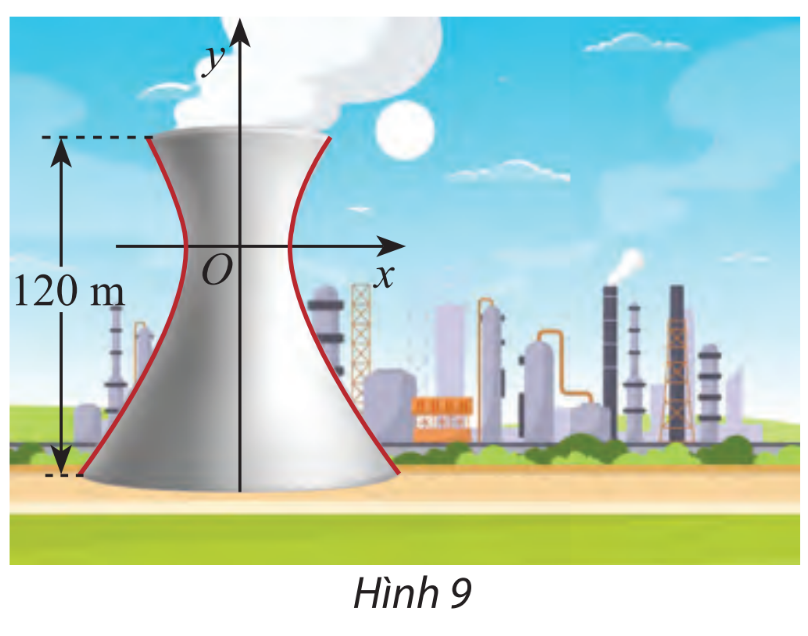

Bước 1: Xác định khoảng cách từ tâm đến đỉnh tháp và đáy tháp
Bước 2: Từ kết quả vừa tìm thay vào phương trình hypebol y bằng kết quả đó tìm x (Chỉ lấy kết quả dương)

Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là z
Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là 2z
Ta có \(z + 2z = 120 \Rightarrow z = 40\)
Thay \(y = 40\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 2 \)
Thay \(y = 80\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 5 \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(27\sqrt 2 \) và \(27\sqrt 5 \)
