HĐ Khởi động

Qua bài học ta thấy rằng hình dạng của các đường là phương trình chính tắc của chúng như sau:
(E) có tên gọi là elip, phương trình: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
(H) có tên gọi là hypebol, phương trình: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
(P) có tên gọi là parabol, phương trình: \({y^2} = 2px\)
HĐ Khám phá 1
Lấy một tấm bìa, ghim hai cái đinh lên đó tại hai điểm \({F_1}\) và \({F_2}\). Lấy một vòng dây kín không đàn hồi có độ dài lớn hơn hai lần đoạn \({F_1}{F_2}\). Quàng vòng dây đó qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một đường mà người ta gọi là đường elip.
Cho biết 2c là khoảng cách \({F_1}{F_2}\) và \(2a + 2c\) là độ dài của vòng dây.
Tính tổng hai khoảng cách \({F_1}M\) và \({F_2}M\)
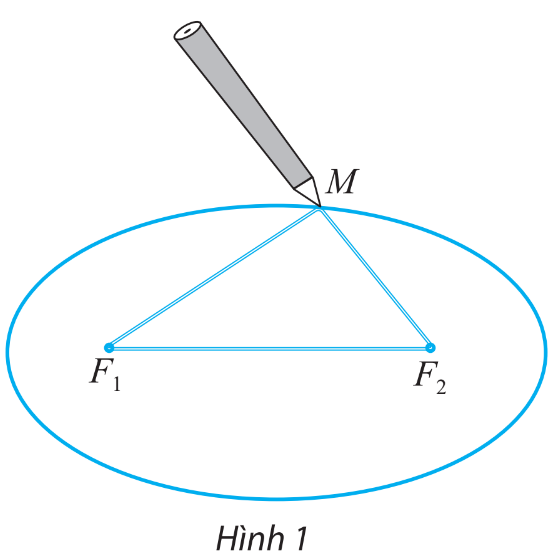

Ta có chiều dài vòng dây là:
\(M{F_1} + {F_1}{F_2} + {F_2}M = 2a + 2c \Rightarrow M{F_1} + {F_2}M = 2a + 2c - {F_1}{F_2} = 2a\)
Vậy tổng khoảng cách \({F_1}M\) và \({F_2}M\) là 2a
HĐ Khám phá 2
Cho elip (E) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (E) \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)
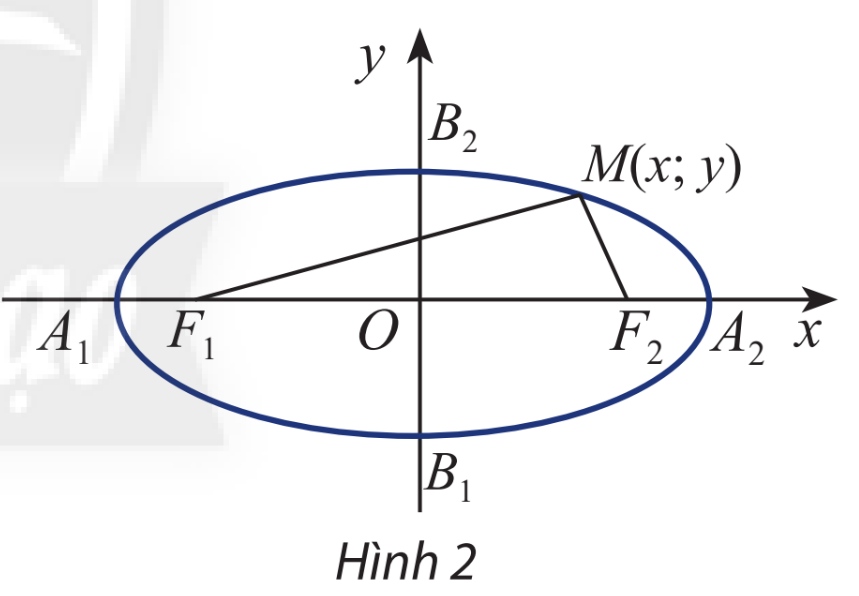

Sử dụng phương pháp tọa độ trong mặt phẳng
Advertisements (Quảng cáo)

a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \({F_1}M + {F_2}M = 2a \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)
Thực hành 1
Viết phương trình chính tắc của elip trong hình 4
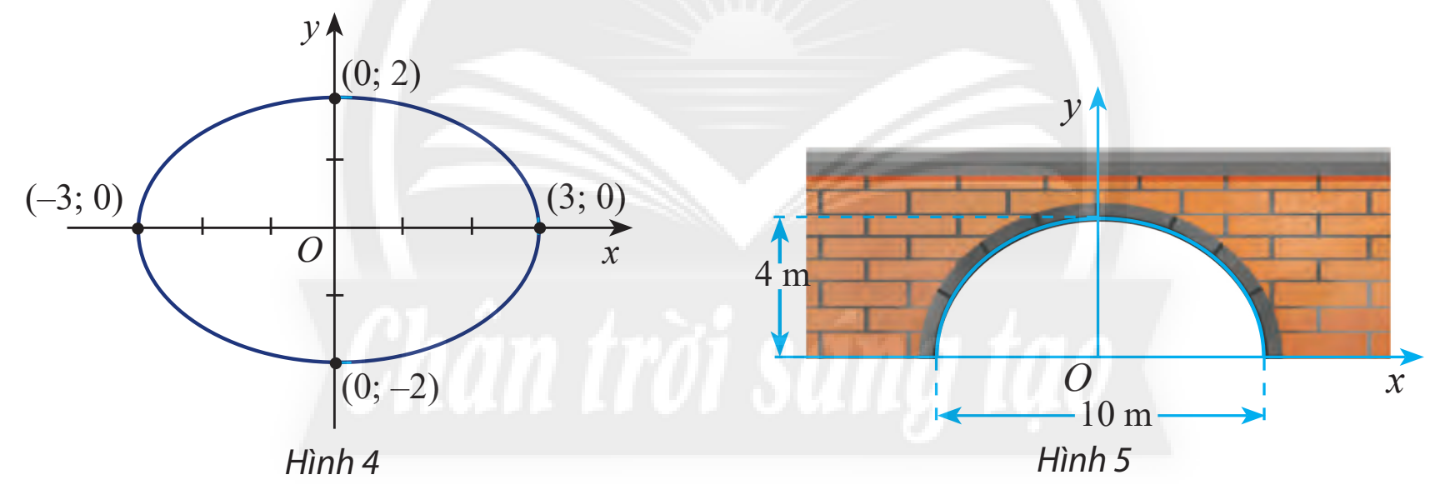

Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (E);b = \sqrt {{a^2} - {c^2}} \)

Dựa vào hình vẽ ta thấy \(a = 3,c = 2 \Rightarrow b = \sqrt {{a^2} - {c^2}} = \sqrt {{3^2} - {2^2}} = \sqrt 5 \)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\)
Vận dụng 1
Một đường hầm có mặt các hình nửa Elip cao 4 m, rộng 10 m (hình 5). Viết phương trình chính tắc của elip đó.

Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (E);b = \sqrt {{a^2} - {c^2}} \)

Chiều cao là 4 m tương ứng với \(c = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Suy ra \(b = \sqrt {{a^2} - {c^2}} = \sqrt {{5^2} - {4^2}} = 3\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\)
