HĐ Khám phá 2
Một người dùng một lực \(\overrightarrow F \) có cường độ là 10 N kéo một chiếc xe đi quãng đường dài 100 m. Tính công sinh bởi lực \(\overrightarrow F \), biết rằng góc giữa vectơ \(\overrightarrow F \) và hướng di chuyển là \(45^\circ \). (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực \(\overrightarrow F \), độ dài quãng đường và côsin các góc giữa vectơ \(\overrightarrow F \) và độ dịch chuyển \(\overrightarrow d \)).
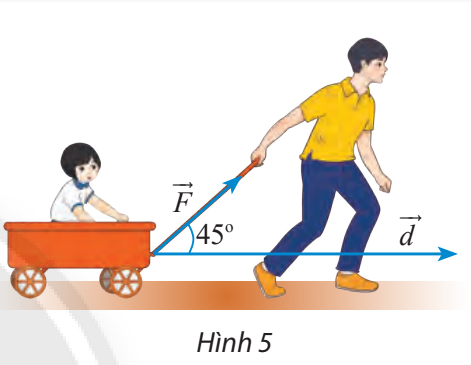

Theo giả thiết ta có: \(A = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right)\)
\( \Rightarrow A = 10.100.\cos 45^\circ = 500\sqrt 2 \left( J \right)\)
Vậy công sinh bởi lực \(\overrightarrow F \) là \(500\sqrt 2 \) (J)
Thực hành 2
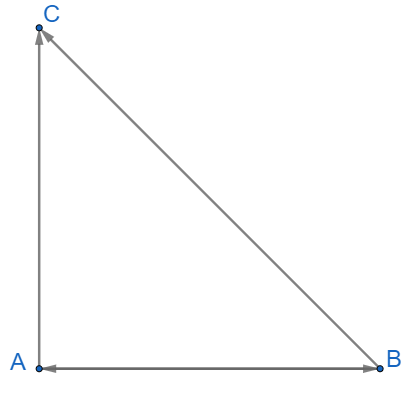
Cho tam giác ABC vuông cân tại A, có cạnh huyền bằng \(\sqrt 2 \).
Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AC} .\overrightarrow {BC} ,\overrightarrow {BA} .\overrightarrow {BC} \)

Bước 1: Vận dụng công thức \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
Bước 2: Xác định độ dài cạnh AB, AC và góc giữa hai vecto \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)

+) Ta có: \(AB \bot AC \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AC} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 0\)
+) \(\overrightarrow {AC} .\overrightarrow {BC} = \left| {\overrightarrow {AC} } \right|.\left| {\overline {BC} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right)\)
Ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt 2 \Leftrightarrow \sqrt {2A{C^2}} = \sqrt 2 \)\( \Rightarrow AC = 1\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BC} = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
+) \(\overrightarrow {BA} .\overrightarrow {BC} = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = 1.\sqrt 2 .\cos \left( {45^\circ } \right) = 1\)
Advertisements (Quảng cáo)
Thực hành 3
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) có độ dài lần lượt là 3 và 8 có tích vô hướng là \(12\sqrt 2 \).Tính góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)

Sử dụng công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\)

Ta có: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
\( \Leftrightarrow 12\sqrt 2 = 3.8.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 2 }}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ \)
Vậy góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là \(45^\circ \)
Vận dụng 1
Một người dùng một lực \(\overrightarrow F \) có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m cùng hướng với \(\overrightarrow F \). Tính công sinh bởi lực \(\overrightarrow F \).

Công thức tính công: \(A = \overrightarrow F .\overrightarrow d \)
Tích vô hướng: \(\overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right)\)

Gọi vectơ dịch chuyển của vật là \(\overrightarrow d \), ta có \(|\overrightarrow d |\; = 50\).
Theo giả thiết \(\overrightarrow F \) và \(\overrightarrow d \) cùng hướng nên \(\left( {\overrightarrow F ,\overrightarrow d } \right) = 0^\circ \)
Công sinh ra bởi lực \(\overrightarrow F \)được tính bằng:
\(A = \overrightarrow F .\overrightarrow d = \left| {\overrightarrow F } \right|.\left| {\overrightarrow d } \right|.\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = 20.50.\cos 0^\circ = 1000\) (J)
