HĐ Khám phá 1
Cho hình vuông ABCD có tâm I (Hình 1).
a) Tính \(\widehat {IDC}\).
b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C
c) Tìm hai vectơ có điểm đầu là D và lần lượt bằng vectơ \(\overrightarrow {IB} \)và \(\overrightarrow {AB} \)


a) I là tâm của ABCD, suy ra \(\widehat {IDC} = 45^\circ \)
b) Vectơ có điểm đầu là D và điểm cuối là I là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và điểm cuối là C là \(\overrightarrow {DC} \)
c) Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {IB} \) là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {DC} \)
Thực hành 1
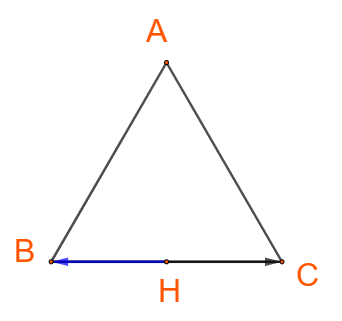
Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc:
\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right),\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right),\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right)\).
Advertisements (Quảng cáo)

Bước 1: Xác định hai vectơ cần tìm góc
Bước 2: Đưa 2 vectơ về cùng điểm đầu (chung gốc)
Bước 3: Xác định góc giữa 2 vectơ, chẳng hạn: \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)

+) \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {ABC} = 60^\circ \)
+) Dựng hình bình hành ABCD, ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD} = 120^\circ \)
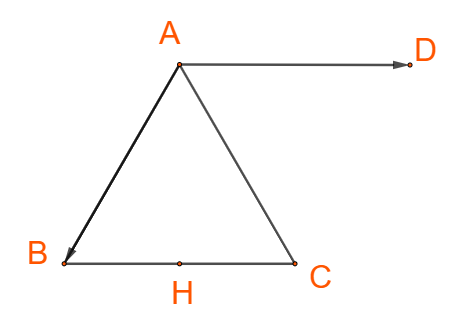
+), Ta có: ABC là tam giác đều, H là trung điểm BC nên \(AH \bot BC\)
\(\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AH} ,\overrightarrow {AD} } \right) = \widehat {HAD} = 90^\circ \)
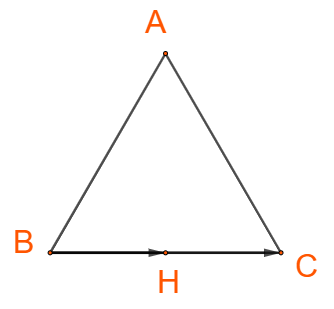
+) Hai vectơ \(\overrightarrow {BH} \) và \(\overrightarrow {BC} \)cùng hướng nên \(\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right) = 0^\circ \)
+) Hai vectơ \(\overrightarrow {HB} \) và \(\overrightarrow {BC} \)ngược hướng nên \(\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right) = 180^\circ \)