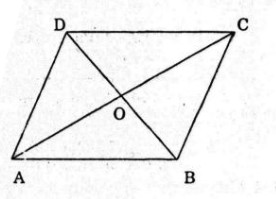
Bài 10. Cho hình bình hành \(ABCD\) với tâm \(O\). Hãy điền vào chỗ trống (…) để được đẳng thức đúng
a) \(\overrightarrow {AB} + \overrightarrow {AD} = ...................\)
b) \(\overrightarrow {AB} + \overrightarrow {CD} = ...................\)
c) \(\overrightarrow {AB} + \overrightarrow {OA} = ...................\)
d) \(\overrightarrow {OA} + \overrightarrow {OC} = ...................\)
e ) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = ...................\)

Advertisements (Quảng cáo)
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (quy tắc hình bình hành).
b) \(\overrightarrow {AB} + \overrightarrow {CD} = \,\overrightarrow {AB} + \overrightarrow {BA} = \overrightarrow 0 \,\)
c) \(\overrightarrow {AB} + \overrightarrow {OA} = \overrightarrow {AB} + \overrightarrow {OB} + \overrightarrow {BA} = \overrightarrow {OB} \) (quy tắc ba điểm).
d) \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \) (vì O là trung điểm của AC).
e) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = (\overrightarrow {OA} + \overrightarrow {OC} ) + (\overrightarrow {OB} + \overrightarrow {OD} ) = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \) (vì O là trung điểm của AC).
