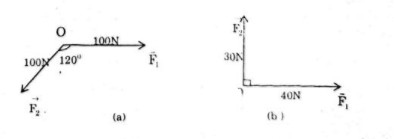
Bài 13. Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cùng có điểm đặt tại \(O\) (h.17). Tìm cường độ lực tổng hợp của chúng trong các trường hợp sau
a) \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều có cường độ là \(100N\), góc hợp bởi \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({120^0}\) (h.17a);
b) Cường độ của \(\overrightarrow {{F_1}} \) là \(40N\), của \(\overrightarrow {{F_2}} \) là \(30N\) và góc giữa \(\overrightarrow {{F_1}} \) và \( \overrightarrow {{F_2}} \) bằng (h.17b).

a)
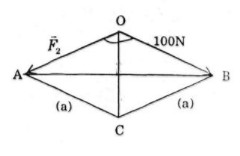
Ta lấy \(\overrightarrow {{F_2}} = \overrightarrow {OA} ,\,\overrightarrow {{F_1}} = \overrightarrow {OB} \).
Theo quy tắc hình bình hành, ta vẽ hình bình hành \(OACB\).
Advertisements (Quảng cáo)
Hình bình hành \(OACB\) có \(OA = OB\) nên \(OACB\) là hình thoi.
Ta có \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \), \(OC\) là phân giác góc \(\widehat {AOB}\) nên \(\widehat {AOC} = {60^0}\). Mà \(OACB\) là hình thoi nên tam giác \(AOC\) đều. Suy ra \(OA = OC\). Vậy cường độ lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là \(100N\).
b)
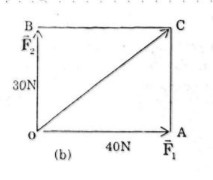
Đặt \(\overrightarrow {OA} = \overrightarrow {{F_1}} ,\overrightarrow {OB} = \overrightarrow {{F_2}} \). \(C\) là đỉnh thứ tư của hình bình hành \(OABC\).
Do góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({90^0}\) suy ra tứ giác \(OABC\) là hình chữ nhật.
\( \Rightarrow OC = \sqrt {O{A^2} + O{B^2}} = \sqrt {{{40}^2} + {{30}^2}} = 50N\)
Ta có: \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Vậy cường độ tổng hợp lực của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là \(50N.\)
