Bài 11. a) Bằng cách sử dụng hằng đẳng thức \(a^2-b^2= (a-b)(a+b)\),
hãy xét dấu \(f(x)= x^4– x^2+6x – 9\) và \(g(x) = x^2– 2x - {4 \over {{x^2} - 2x}}\)
b) Hãy tìm nghiệm nguyên của bất phương trình sau: \(x(x^3– x + 6) > 9\)
a) \(f(x) = {x^4} - {x^2} + 6x - 9 = {\left( {{x^2}} \right)^2} - {\left( {x - 3} \right)^2} = \left( {{x^2} + x - 3} \right)\left( {{x^2} - x + 3} \right)\)
\({{x^2} - x + 3} > 0, ∀x ∈\mathbb R\) ( vì \(a = 1> 0, Δ = 1- 4.3<0\))
Suy ra \(f(x)>0\) với \(x < {{ - 1 - \sqrt {13} } \over 2}\) hoặc \(x > {{ - 1 + \sqrt {13} } \over 2}\)
\(g(x) = x^2– 2x - {4 \over {{x^2} - 2x}}\)
= \({{{{({x^2} - 2x)}^2} - {2^2}} \over {{x^2} - 2x}} = {{({x^2} - 2x + 2)({x^2} - 2x - 2)} \over {{x^2} - 2x}}\)
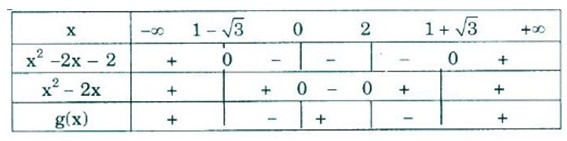
Bởi vì \(x^2– 2x + 2 > 0 ,∀x ∈\mathbb R\) nên dấu của \(g(x)\) là dấu của \({{{x^2} - 2x - 2} \over {{x^2} - 2x}}\)
Advertisements (Quảng cáo)
Lập bảng xét dấu:
b)
\(\eqalign{
& x({x^3} - x + 6) > 9 \Leftrightarrow {x^4} - {x^2} + 6x - 9 > 0 \cr
& \Leftrightarrow {x^4} - {(x - 3)^2} > 0 \Leftrightarrow ({x^2} - x + 3)({x^2} + x - 3) > 0 (1) \cr} \)
Vì \({{x^2} - x + 3} > 0, ∀x ∈\mathbb R\) ( vì \(a = 1> 0, Δ = 1- 4.3<0\))
Do đó (1) \(\Leftrightarrow ({x^2} + x - 3) > 0 \)
\( \Leftrightarrow \left[ \matrix{
x < {{ - 1 - \sqrt {13} } \over 2} \hfill \cr
x > {{ - 1 + \sqrt {13} } \over 2} \hfill \cr} \right.\)
Vậy nghiệm nguyên của bất phương trình là \(\left\{x\in \mathbb Z|x\le-3\text{ hoặc } x\ge2\right\}\)
