Một vật đặt trên mặt phẳng nghiêng (góc nghiêng α = 300) , được truyền một vận tốc ban đầu \({v_0} = 2m/s\)(Hình 23.4). Hệ số ma sát giữa vật và mặt phẳng nghiêng là 0,3.
a) Tính gia tốc của vật.
b) Tính độ cao lớn nhất (H) mà vật đạt tới.
c) Sau khi đạt tới độ cao H, vật sẽ chuyển động như thế nào ?

\(\alpha = {30^0}\,;{v_0} = 2m/s;{\mu _t} = 0,3\)
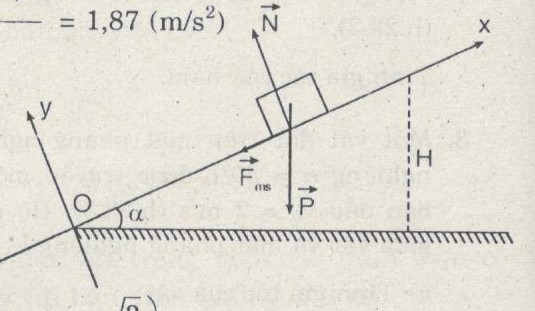
Chọn gốc tọa độ O là điểm truyền vận tốc v0, chiều trục như hình vẽ.
Advertisements (Quảng cáo)
a) Gia tốc của vật:
\(\eqalign{ & a = - g\left( {\sin \alpha + {\mu _t}{\rm{cos}}\alpha } \right) = - 9,8\left( {0,5 + 0,3{{\sqrt 3 } \over 2}} \right) \cr & a = - 7,45(m/{s^2}) \cr} \)
b) Khi đạt độ cao cực đại thì vật có v = 0 nên quãng đường đi được tới lúc đó là
\(\eqalign{ & S = {{ - v_0^2} \over {2a}} \cr & \,{H_{\max }} = S.\sin \alpha = {{ - {v_0}^2\sin \alpha } \over {2a}} = {{ - {2^2}.0,5} \over {2.( - 7,45)}}\cr&\;\;\;\;\;\;\;\;\;\;\; \approx 0,134(m) = 13,4cm \cr} \).
c) Coi \({\mu _n} = {\mu _t} = 0,3\). Tại vị trí cao nhất, lực ma sát chuyển thành ma sát nghỉ, chiều dương hướng lên.
So sánh hai thành phần lực Px và Fmsn ta thấy:
\({{{P_x}} \over {{F_{ms}}}} = {{mg\sin \alpha } \over {{\mu _n}mg\cos \alpha }}\, = {{\tan \alpha } \over {{\mu _n}}}\, = {1 \over {0,3\sqrt 3 }} > 1\)
Vậy vật đổi chiều chuyển động, chuyển động nhanh dần đều xuống với gia tốc khác:
\({a’} = - g(\sin \alpha - {\mu _t}{\rm{cos}}\alpha {\rm{)}} \approx {\rm{ - 0,19(m/}}{{\rm{s}}^2})\)
