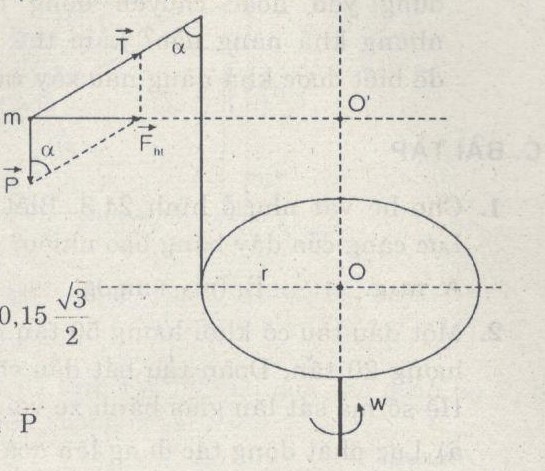
Một con lắc gồm một quả cầu nhỏ khối lượng m = 200 g treo vào sợi dây chiều dài l = 15 cm, buộc vào đầu một cái cọc gắn với mép một cái bàn quay (Hình 23.5). Bàn có bán kính r = 20 cm và quay với vận tốc không đổi.
a) Tính số vòng quay của bàn trog 1 min để dây nghiêng so với phương thẳng đứng một góc \(\alpha = {60^0}\).
b) Tính lực căng của dây trong trường hợp của câu a).

a) Khi bàn quay đều với vận tốc góc \(\omega \) thì chất điểm m chuyển động tròn đều trên một đường tròn nằm ngang tâm O’.
Bán kính quỹ đạo:
Advertisements (Quảng cáo)
\(\eqalign{ & R = r + l\sin \alpha = 0,2 + 0,15{{\sqrt 3 } \over 2} \cr & R \approx 0,33\,m \cr} \)
Lực hướng tâm là hợp của \(\overrightarrow P \,và\,\overrightarrow T \,nên\,\overrightarrow {{F_{ht}}} = \overrightarrow P + \overrightarrow T \)
\(\eqalign{ & = > {F_{ht}} = P.\tan \alpha < = > mR{\omega ^2} = mg.\tan \alpha \cr& < = > R{(2\pi f)^2} = g\tan \alpha \cr & = > f = {1 \over {2\pi }}\sqrt {{{g\tan \alpha } \over R}} = {1 \over {2.3,14}}.\sqrt {{{9,8.\sqrt 3 } \over {0,33}}} \cr&\;\;\;\;\;\;\;\;\;\;=1,142\;Hz \cr} \)
Số vòng quay trong 1 min: \(n = 60f = 68,5\) (v/min)
b) Lực căng dây: \(T = {P \over {{\rm{cos}}\alpha }} = {{mg} \over {{\rm{cos}}\alpha }} = {{0,2.9,8} \over {0,5}} = 3,92(N)\)