Hai bến sông A và B cách nhau 18 km theo đường thẳng . Một chiếc ca nô phải mất bao nhiêu thời gian để đi từ A đến B rồi trở lại ngay từ B về A ? Biết rằng vận tốc của ca nô khi nước không chảy là 16 ,2 km/h và vận tốc của dòng nước so với bờ sông là 1,5 m/s
Giải :
Coi Ca nô là vật 1
Nước là vật 2
Bờ là vật 3
Chọn chiều dương như hình vẽ
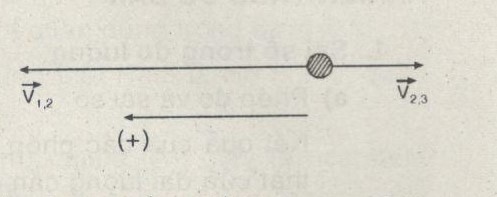
* Khi xuôi dòng :
Với \({v_{12}} = 16,2km/h;{v_{23}} = 5,4km/h\)
* Khi ngược dòng :
Advertisements (Quảng cáo)
Với \({v_{12}} = 16,2km/h;{v_{23}} = - 5,4km/h\)
Áp dụng công thức vận tốc trong chuyển động thẳng đều và công thức cộng vận tốc :
Khi xuôi: \({{AB} \over {{t_1}}} = {v_{13}} = {v_{12}} + {v_{23}} \)
\(= > {t_1} = {{AB} \over {{v_{12}} + {v_{23}}}} = {{18} \over {16,2 + 5,4}} = {5 \over 6}(h)\)
Khi ngược :
\(\eqalign{ & {{AB} \over {{t_2}}} = {v_{13}} = {v_{12}} + {v_{23}}\cr&= > {t_2} = {{18} \over {16,2 - 5,4}} = {{5} \over 3}(h) \cr & t = {t_1} + {t_2} = 2,5h \cr} \)
Chú ý :
- Các đại lượng trong công thức \({v_{13}} = {v_{12}} + {v_{23}}\) là các đại lượng đại số.
- Nếu chọn chiều dương là chiều chuyển động của thuyền so với bờ để có độ dời ∆x = quãng đường S.
-Nếu biểu diễn các vectơ đã biết phương chiều \(\left( {\overrightarrow {{v_{23}}} ;\overrightarrow {{v_{12}}} } \right)\) vectơ nào cùng chiều dương sẽ có giá trị đại số dương và ngược lại.
