
Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của các cạnh \(AB\), \(AD\) và \(P\) là một điểm nằm trên \(CD\). Đường thẳng \(BC\) cắt mặt phẳng \(\left( {MNP} \right)\) tại \(Q\). Chứng minh rằng \(PQ\parallel BD\).

Chứng minh rằng \(MN\parallel BD\).
Xét ba mặt phẳng \(\left( {MNP} \right)\), \(\left( {ABD} \right)\) và \(\left( {BCD} \right)\), sử dụng định lý về giao tuyến của 3 mặt phẳng.

Advertisements (Quảng cáo)
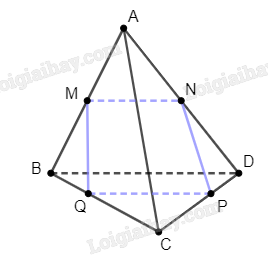
Ta có \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AD\), nên \(MN\) là đường trung bình của tam giác \(ABD\). Suy ra \(MN\parallel BD\).
Xét ba mặt phẳng \(\left( {MNP} \right)\), \(\left( {ABD} \right)\) và \(\left( {BCD} \right)\), ta có \(MN\) là giao tuyến của \(\left( {ABD} \right)\) và \(\left( {MNP} \right)\); \(PQ\) là giao tuyến của \(\left( {BCD} \right)\) và \(\left( {MNP} \right)\), \(BD\) là giao tuyến của \(\left( {ABD} \right)\) và \(\left( {BCD} \right)\).
Mà \(MN\parallel BD\), nên theo định lý về giao tuyến của ba mặt phẳng, ta suy ra \(PQ\parallel BD\).
Bài toán được chứng minh.
