
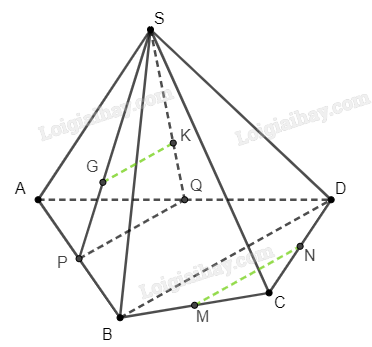
Cho hình chóp tứ giác \(S.ABCD\). Gọi \(G\), \(K\) lần lượt là trọng tâm của các tam giác \(SAB\) và \(SAD\); \(M\), \(N\) lần lượt là trung điểm của các cạnh \(BC\) và \(CD\). Chứng minh rằng \(GK\parallel MN\).

Gọi \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\). Chứng minh rằng các đường thẳng \(GK\), \(PQ\), \(BD\), \(MN\) đôi một song song với nhau, từ đó suy ra điều phải chứng minh.

Gọi \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\).
Advertisements (Quảng cáo)
Ta có \(G\) là trọng tâm của tam giác \(SAB\), nên suy ra \(G \in SP\) và \(\frac{{SG}}{{SP}} = \frac{2}{3}\).
Chứng minh tương tự ta cũng có \(K \in SQ\) và \(\frac{{SK}}{{SQ}} = \frac{2}{3}\).
Tam giác \(SPQ\) có \(\frac{{SG}}{{SP}} = \frac{{SK}}{{SQ}}\) nên theo định lý Thales ta có \(GK\parallel PQ\).
Xét tam giác \(ABD\), ta có \(P\) là trung điểm của \(AB\), \(Q\) là trung điểm của \(AD\), nên \(PQ\) là đường trung bình của tam giác \(ABD\). Suy ra \(PQ\parallel BD\).
Chứng minh tương tự ta cũng có \(MN\parallel BD\).
Từ đó suy ra \(GK\parallel MN\). Bài toán được chứng minh.
