
Cho \(a\), \(b\) là hai đường thẳng phân biệt cắt ba mặt phẳng song song \(\left( P \right)\), \(\left( Q \right)\), \(\left( R \right)\) lần lượt tại \(A,{\rm{ }}B,{\rm{ }}C\) và \(A’,{\rm{ }}B’,{\rm{ }}C’\). Khẳng định nào sau đây là SAI?
A. \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{CA}}{{C’A’}}\)
B. \(\frac{{A’B’}}{{AB}} = \frac{{B’C’}}{{BC}} = \frac{{C’A’}}{{CA}}\)
C. \(\frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}}\)
D. \(\frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}} = \frac{{AC}}{{A’C’}}\)

Advertisements (Quảng cáo)
Sử dụng định lý Thales.

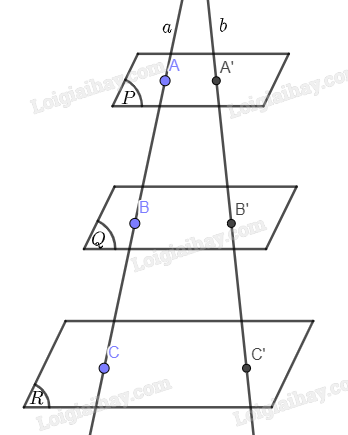
Áp dụng định lý Thales, ta có \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{CA}}{{C’A’}}\). Như vậy, đáp án A đúng. Tương tự đáp án B cũng đúng.
Do \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} \Rightarrow \frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}}\), suy ra đáp án C đúng.
Đáp án D sai vì \(\frac{{AB}}{{BC}} \ne \frac{{AC}}{{A’C’}}\).
Vậy đáp án cần chọn là đáp án D.
