
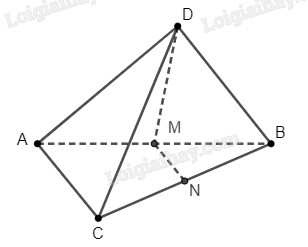
Cho tứ diện \(ABCD\). Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AB,{\rm{ }}CD\). Chứng minh rằng bốn điểm \(M,{\rm{ }}N,{\rm{ }}C,{\rm{ }}D\) không cùng nằm trong một mặt phẳng.

Giả sử 4 điểm \(M\), \(N\), \(C\), \(D\) cùng nằm trong một mặt phẳng.
Từ đó chứng minh rằng \(M \in \left( {BCD} \right)\), suy ra \(A \in \left( {BCD} \right)\) và suy ra điều vô lí.

Advertisements (Quảng cáo)
Do \(N\) là trung điểm của \(BC\), nên 4 điểm \(B\), \(N\), \(C\), \(D\) cùng nằm trong mặt phẳng.
Giả sử 4 điểm \(M\), \(N\), \(C\), \(D\) cùng nằm trong một mặt phẳng.
Điều này có nghĩa là \(M \in \left( {NCD} \right)\).
Do bốn điểm \(B\), \(N\), \(C\), \(D\) cùng nằm trong mặt phẳng, ta suy ra \(M \in \left( {BCD} \right)\).
Điểm \(M\) và điểm \(B\) cùng nằm trong mặt phẳng \(\left( {BCD} \right)\), nên \(BM \subset \left( {BCD} \right)\).
Mặt khác, do \(M\) là trung điểm của \(AB\), nên \(A \in BM\).
Suy ra \(A \in \left( {BCD} \right)\). Điều này là vô lý do \(ABCD\) là tứ diện nên bốn điểm \(A\), \(B\), \(C\), \(D\) không cùng nằm trong một mặt phẳng.
