
Cho hai mặt phẳng \(\left( P \right),{\rm{ }}\left( Q \right)\) cắt nhau theo giao tuyến \(d\) và hai đường thẳng \(a,{\rm{ }}b\) lần lượt nằm trong \(\left( P \right),{\rm{ }}\left( Q \right)\). Chứng minh rằng nếu hai đường thẳng \(a,{\rm{ }}b\) cắt nhau thì giao điểm của chúng thuộc đường thẳng \(d\).

Gọi \(I\) là giao điểm của hai đường thẳng \(a\) và \(b\). Chỉ ra rằng \(I\) thuộc cả hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\), từ đó suy ra \(I \in d\).

Advertisements (Quảng cáo)
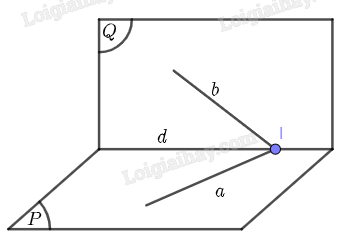
Gọi \(I\) là giao điểm của hai đường thẳng \(a\) và \(b\). Suy ra \(\left\{ \begin{array}{l}I \in a\\I \in b\end{array} \right.\)
Vì \(a \subset \left( P \right)\) và \(b \subset \left( Q \right)\), ta suy ra \(\left\{ \begin{array}{l}I \in \left( P \right)\\I \in \left( Q \right)\end{array} \right.\), tức là \(I\) thuộc giao tuyến của hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Mà \(\left( P \right) \cap \left( Q \right) = d\), suy ra \(I \in d\).
Bài toán được chứng minh.
