
Hình biểu diễn của hai đường thẳng cắt nhau có thể là hai đường thẳng song song được không? Vì sao?

Giả sử hai đường thẳng \(a\) và \(b\) cắt nhau tại \(O\) và hình chiếu song song của \(a\), \(b\), \(O\) theo phương chiếu là đường thẳng bất kỳ \(c\) lần lượt là \(a’\), \(b’\), \(O’\). Ta cần xác định xem \(a’\) và \(b’\) có song song với nhau không.

Advertisements (Quảng cáo)
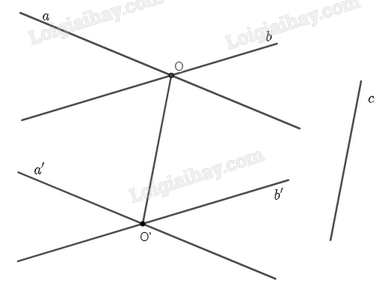
Giả sử hai đường thẳng \(a\) và \(b\) cắt nhau tại \(O\) và hình chiếu song song của \(a\), \(b\), \(O\) theo phương chiếu là đường thẳng bất kỳ \(c\) lần lượt là \(a’\), \(b’\), \(O’\).
Ta nhận xét rằng với mỗi điểm \(M \in a\) thì hình chiếu song song \(M’\) của \(M\) theo phương chiếu \(c\) cũng nằm trên \(a’\). Do đó, vì \(O \in a\) nên ta có \(O’ \in a’\).
Tương tự ta cũng có \(O’ \in b’\). Như vậy \(a’\) và \(b’\) có điểm chung \(O’\), nên chúng không song song với nhau.
Vậyhình biểu diễn của hai đường thẳng cắt nhau không thể là hai đường thẳng song song.
