
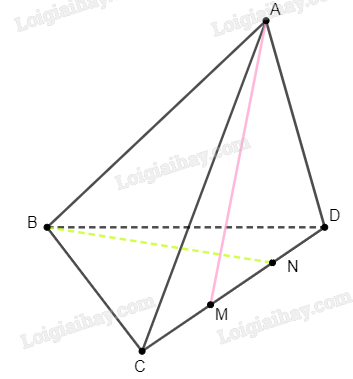
Cho tứ diện \(ABCD\). Trên cạnh \(CD\) lấy hai điểm \(M\) và \(N\) khác nhau. Chứng minh rằng các đường thẳng \(AM\) và \(BN\) không cắt nhau.

Chứng minh bằng phương pháp “phản chứng”: Giả sử \(AM\) cắt \(BN\), ta sẽ chứng minh được \(A\), \(B\), \(C\), \(D\) đồng phẳng, và đây là điều vô lí. Từ đó suy ra điều phải chứng minh.

Advertisements (Quảng cáo)
Giả sử \(AM\) cắt \(BN\). Như vậy tồn tại mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(AM\) và \(BN\).
Do \(M\) và \(N\) cùng nằm trên \(\left( P \right)\), ta suy ra đường thẳng \(MN\) cũng nằm trên \(\left( P \right)\). Từ đó \(C\) và \(D\) cũng thuộc \(\left( P \right)\).
Như vậy \(A\), \(B\), \(C\), \(D\) cùng thuộc mặt phẳng \(\left( P \right)\). Điều này là vô lí, do với mọi tứ diện \(ABCD\) thì 4 điểm \(A\), \(B\), \(C\), \(D\) luôn không đồng phẳng.
Do đó điều giả sử là sai.
Vậy hai đường thẳng \(AM\) và \(BN\) không cắt nhau.
