
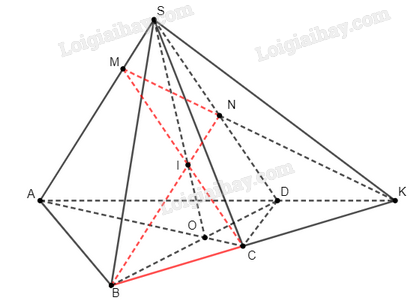
Cho hình chóp tứ giác \(S.ABCD\) có đáy không là hình thang. Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Trên \(SO\) lấy điểm \(I\) sao cho \(SI = 2IO\).
a) Xác định các giao điểm \(M\), \(N\) lần lượt của \(SA\), \(SD\) với mặt phẳng \(\left( {IBC} \right)\).
b*) Chứng minh rằng các đường thẳng \(AD\), \(BC\) và \(MN\) đồng quy.

a) Để xác định giao điểm của mặt phẳng với một đường thẳng cho trước, ta cần chọn một đường thẳng khác nằm trong mặt phẳng đã cho, rồi tìm giao điểm của 2 đường thẳng đó.
b) Gọi \(K\) là giao điểm của \(AD\) và \(BC\). Ta cần chứng minh \(MN = \left( {IBC} \right) \cap \left( {SAD} \right)\). Từ đó suy ra \(K \in MN\).

a)
Giao điểm \(M\) của \(SA\) và \(\left( {IBC} \right)\):
Ta nhận xét rằng \(I \in SO \subset \left( {SAC} \right) \Rightarrow CI \subset \left( {SAC} \right)\).
Trên mặt phẳng \(\left( {SAC} \right)\), gọi \(\left\{ M \right\} = CI \cap SA\).
Advertisements (Quảng cáo)
Do \(IC \subset \left( {IBC} \right)\), nên \(\left\{ M \right\} = \left( {IBC} \right) \cap SA\).
Vậy \(M\) là giao điểm của \(\left( {IBC} \right)\) và \(SA\).
Giao điểm \(N\) của \(SD\) và \(\left( {IBC} \right)\):
Ta nhận xét rằng \(I \in SO \subset \left( {SBD} \right) \Rightarrow BI \subset \left( {SBD} \right)\).
Trên mặt phẳng \(\left( {SBD} \right)\), gọi \(\left\{ N \right\} = BI \cap SD\).
Do \(IB \subset \left( {IBC} \right)\), nên \(\left\{ N \right\} = \left( {IBC} \right) \cap SD\).
Vậy \(N\) là giao điểm của \(\left( {IBC} \right)\) và \(SD\).
b) Trên mặt phẳng \(\left( {ABCD} \right)\), gọi \(K\) là giao điểm của \(AD\) và \(BC\).
Ta có \(\left\{ \begin{array}{l}M \in SA \subset \left( {SAD} \right)\\M \in \left( {IBC} \right)\end{array} \right. \Rightarrow M \in \left( {SAD} \right) \cap \left( {IBC} \right)\).
Mặt khác, \(\left\{ \begin{array}{l}N \in SD \subset \left( {SAD} \right)\\N \in \left( {IBC} \right)\end{array} \right. \Rightarrow N \in \left( {SAD} \right) \cap \left( {IBC} \right)\).
Vậy giao tuyến của \(\left( {SAD} \right)\) và \(\left( {IBC} \right)\) là đường thẳng \(MN\).
Do \(AD \in \left( {SAD} \right)\), \(BC \in \left( {IBC} \right)\), \(\left\{ K \right\} = AD \cap BC\), ta suy ra \(K\) nằm trên giao tuyến của \(\left( {SAD} \right)\) và \(\left( {IBC} \right)\), tức là \(K \in MN\).
Vậy ba đường thẳng \(AD\), \(BC\), \(MN\) cắt nhau tại \(K\).
