
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Chứng minh rằng:
a) \(BC \bot \left( {OAH} \right)\).
b) H là trực tâm của \(\Delta ABC\).
c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).

Sử dụng kiến thức về đường thẳng vuông góc với mặt phẳng:
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau trong \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
+ Nếu đường thẳng d vuông góc với mặt phẳng \(\left( \alpha \right)\) thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng \(\left( \alpha \right)\).

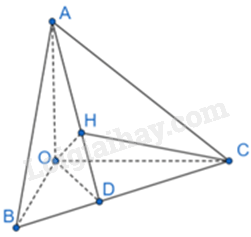
a) Vì H là hình chiếu của O trên mặt phẳng (ABC) nên \(OH \bot \left( {ABC} \right) \Rightarrow OH \bot BC\)
Vì \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {BOC} \right) \Rightarrow OA \bot BC\)
Advertisements (Quảng cáo)
Ta có: \(OA \bot BC,OH \bot BC \Rightarrow BC \bot \left( {OAH} \right)\)
b) Vì \(BC \bot \left( {OAH} \right)\) nên \(BC \bot AH\) (1)
Vì \(OH \bot \left( {ABC} \right) \Rightarrow OH \bot AC\)
Vì \(OA \bot OB,OB \bot OC \Rightarrow OB \bot \left( {AOC} \right) \Rightarrow OB \bot AC\)
Ta có: \(OB \bot AC,OH \bot AC \Rightarrow AC \bot \left( {OBH} \right) \Rightarrow AC \bot BH\) (2)
Mà H là giao điểm của BH và CH (3)
Từ (1), (2) và (3) ta có: H là trực tâm của \(\Delta ABC\).
c) Gọi D là giao điểm của AH và BC. Khi đó, \(OD \bot BC\)
Vì \(OA \bot \left( {BOC} \right) \Rightarrow OA \bot OD\)
Do đó, tam giác AOD vuông tại O. Mà OH là đường cao nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{D^2}}} + \frac{1}{{O{A^2}}}\)
Tam giác BOC vuông tại O, đường cao OD có: \(\frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Vậy \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
