Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(SA = a\sqrt 3 ,SA \bot AC,\) \(SA \bot BC,\) \(\widehat {BAD} = {120^0}\). Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:
a) SD và BC.
b) MN và SC.
Sử dụng kiến thức về góc giữa hai đường thẳng trong không gian để tính: Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b), là góc giữa hai đường thẳng \(a’\) và \(b’\) cùng đi qua một điểm và lần lượt song song hoặc trùng với a và b.
Góc giữa hai đường thẳng nhận giá trị từ \({0^0}\) đến \({90^0}\).
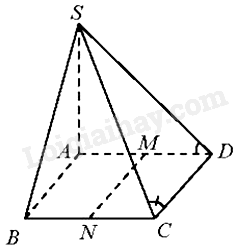
a) Vì ABCD là hình thoi nên AD//BC. Do đó, \(\left( {SD,BC} \right) = \left( {SD,AD} \right) = \widehat {SDA}\)
Vì \(SA \bot BC,\) AD//BC nên \(SA \bot AD\). Do đó, tam giác SAD vuông tại A.
Do đó, \(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^0}\)
b) Vì M, N lần lượt là trung điểm của AD, BC nên MN//CD
Do đó, \(\left( {MN,SC} \right) = \left( {CD,SC} \right) = \widehat {SCD}\)
Áp dụng định lý Pythagore vào tam giác SAD vuông tại A có: \(SD = \sqrt {S{A^2} + A{D^2}} = \sqrt {3{a^2} + {a^2}} = 2a\)
Vì ABCD là hình thoi nên \(AD = DC\). Do đó, tam giác ACD cân tại D
Vì ABCD là hình thoi nên AC là tia phân giác góc BAD. Do đó, \(\widehat {DAC} = \frac{1}{2}\widehat {BAD} = {60^0}\)
Suy ra, tam giác ACD đều nên \(AC = a\)
Áp dụng định lý Pythagore vào tam giác SAC vuông tại A có: \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {3{a^2} + {a^2}} = 2a\)
Áp dụng định lý cosin vào tam giác SCD có:
\(\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2.SC.CD}} = \frac{{{{\left( {2a} \right)}^2} + {a^2} - {{\left( {2a} \right)}^2}}}{{2.2a.a}} = \frac{1}{4} \Rightarrow \widehat {SCD} \approx 75,{5^0}\)