
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Tính góc giữa AB và DM.

Sử dụng kiến thức về góc giữa hai đường thẳng trong không gian để tính: Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b), là góc giữa hai đường thẳng \(a’\) và \(b’\) cùng đi qua một điểm và lần lượt song song hoặc trùng với a và b.
Góc giữa hai đường thẳng nhận giá trị từ \({0^0}\) đến \({90^0}\).

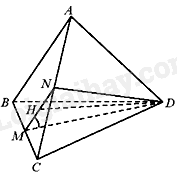
Gọi độ dài cạnh của tứ diện đều ABCD là 2a nên \(MB = MC = \frac{{BC}}{2} = a\)
Gọi N là trung điểm của AC nên \(NA = NC = \frac{{AC}}{2} = a\)
Vì MN là đường trung bình của tam giác ABC nên MN//AB
Advertisements (Quảng cáo)
Do đó, \(\left( {AB,DM} \right) = \left( {MN,MD} \right) = \widehat {NMD}\)
Tam giác CBD đều nên MD là đường trung tuyến đồng thời là đường cao.
Do đó, \(MD \bot BC\). Áp dụng định lý Pythagore vào tam giác MDC vuông tại M có: \(MD = \sqrt {C{D^2} - M{C^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
Tam giác ADC đều nên ND là đường trung tuyến đồng thời là đường cao.
Do đó, \(ND \bot AC\). Áp dụng định lý Pythagore vào tam giác NDC vuông tại N có: \(ND = \sqrt {C{D^2} - N{C^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
Tam giác MND có: \(ND = MD\) nên tam giác MND cân tại D.
Gọi H là trung điểm của MN.
Suy ra DH là đường là đường trung tuyến đồng thời là đường cao của tam giác MND.
Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{{BA}}{2} = a \Rightarrow MH = \frac{{MN}}{2} = \frac{a}{2}\)
Tam giác MHD vuông tại H có: \(\cos \widehat {HMD} = \frac{{MH}}{{MD}} = \frac{{\frac{a}{2}}}{{a\sqrt 3 }} = \frac{{\sqrt 3 }}{6} \Rightarrow \widehat {NMD} \approx 73,{2^0}\)
