
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Tính khoảng cách giữa hai đường thẳng MN và B’D’.

Sử dụng kiến thức về khoảng cách giữa hai đường thẳng chéo nhau để tính: Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó, kí hiệu d(a, b).

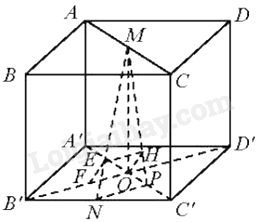
Gọi O là giao điểm của B’D’ và A’C’. Gọi P là trung điểm của OC’.
Advertisements (Quảng cáo)
Vẽ \(OH \bot MP,HE//NP,EF//OH\) (H thuộc MP, E thuộc MN, F thuộc B’D’)
Chứng minh được \(B’D’ \bot \left( {A’C’CA} \right)\) nên \(B’D’ \bot OH\), mà \(EF//OH\) nên \(EF \bot B’D’\left( 1 \right)\)
Vì NP//B’D’ nên \(NP \bot \left( {A’C’CA} \right) \Rightarrow NP \bot OH\), mà \(OH \bot MP\) nên \(OH \bot \left( {MNP} \right)\) hay \(OH \bot MN\), mà \(EF//OH\)\( \Rightarrow EF \bot MN\left( 2 \right)\)
Từ (1) và (2) ta có: \(d\left( {MN,B’D’} \right) = EF = OH\)
Tam giác MOP vuông tại O, ta có: \(OM = a,OP = \frac{1}{2}OC’ = \frac{1}{4}A’C’ = \frac{{a\sqrt 2 }}{4}\) nên
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{P^2}}} + \frac{1}{{O{M^2}}} = {\left( {\frac{4}{{a\sqrt 2 }}} \right)^2} + \frac{1}{{{a^2}}} = \frac{9}{{{a^2}}}\)\( \Rightarrow OH = \frac{a}{3}\)
