Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của SC.
a) Tính khoảng cách từ S đến mặt phẳng (ABC).
b) Tính khoảng cách từ M đến mặt phẳng (SAG).
Sử dụng kiến thức về khoảng cách từ điểm đến mặt phẳng để tính: Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn thẳng MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M; (P)).
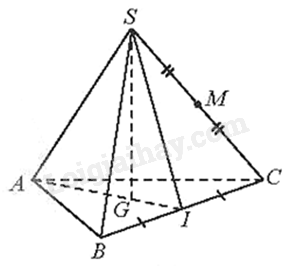
a) Vì S.ABC là hình chóp tam giác đều, G là trọng tâm của tam giác ABC nên \(SG \bot \left( {ABC} \right)\). Do đó, \(d\left( {S;\left( {ABC} \right)} \right) = SG\)
Vì tam giác ABC đều nên \(\widehat {ABC} = {60^0}\).
Gọi I là giao điểm của AG và BC. Khi đó, \(AG = \frac{2}{3}AI\)
Tam giác ABC đều nên AI là đường trung tuyến đồng thời là đường cao. Do đó, tam giác ABI vuông tại I. Suy ra: \(AI = AB.\sin \widehat {ABC} = \frac{{3a\sqrt 3 }}{2} \Rightarrow AG = a\sqrt 3 \)
Vì \(SG \bot \left( {ABC} \right),AG \subset \left( {ABC} \right) \Rightarrow SG \bot AG\)
Áp dụng định lý Pythagore vào tam giác ASG vuông tại G có:
\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{{\left( {2a} \right)}^2} - {{\left( {a\sqrt 3 } \right)}^2}} = a\)
b) Vì \(SC \cap \left( {SAG} \right) = S \) \(\Rightarrow \frac{{d\left( {M,\left( {SAG} \right)} \right)}}{{d\left( {C,\left( {SAG} \right)} \right)}} = \frac{{MS}}{{CS}} = \frac{1}{2} \) \(\Rightarrow d\left( {M,\left( {SAG} \right)} \right) = \frac{1}{2}d\left( {C,\left( {SAG} \right)} \right)\)
Vì \(CB \bot AI,CB \bot SG \Rightarrow CB \bot \left( {SAG} \right)\). Mà \(CB \cap \left( {SAG} \right) = I\)
Do đó, \(d\left( {C,\left( {SAG} \right)} \right) = CI = \frac{1}{2}BC = \frac{{3a}}{2}\). Vậy \(d\left( {M,\left( {SAG} \right)} \right) = \frac{{3a}}{4}\)