
Cho hình chóp tam giác S.ABC có tam giác ABC vuông cân tại B, \(AC = a\sqrt 2 \), mặt phẳng (SAC) vuông góc với mặt đáy (ABC). Các mặt bên (SAB), (SBC) tạo với mặt đáy các góc bằng nhau và bằng \({60^0}\). Tính theo a thể tích V của khối chóp S. ABC

Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)

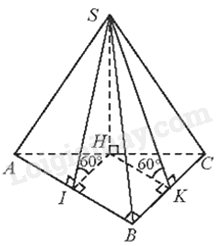
Trong mặt phẳng (SAC), vẽ \(SH \bot AC\left( {H \in AC} \right)\). Vì \(\left( {SAC} \right) \bot \left( {ABC} \right)\) và AC là giao tuyến của hai mặt phẳng (SAC) và (ABC) nên \(SH \bot \left( {ABC} \right)\).
Advertisements (Quảng cáo)
Gọi I, K lần lượt là hình chiếu vuông góc của H lên AB và BC.
Khi đó, \(\left( {\left( {SAB} \right),\left( {ABC} \right)} \right) = \widehat {SIH} = {60^0}\), \(\left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \widehat {SKH} = {60^0}\)
Chứng minh được \(\Delta SHI = \Delta SHK\left( {cgv - gn} \right) \) \(\Rightarrow HI = HK\)
Tứ giác BIHK có: \(\widehat {IBK} = \widehat {BKH} = \widehat {BIH} = {90^0}\) và \(HI = HK\) nên tứ giác BIHK là hình vuông. Suy ra, H là trung điểm của AC. Khi đó, tứ giác BIHK là hình vuông cạnh \(\frac{a}{2}\).
Tam giác SHI vuông tại H nên \(SH = HI.\tan \widehat {SIH} = \frac{{a\sqrt 3 }}{2}\)
Do đó, thể tích V của khối chóp S.ABC là: \(V = \frac{1}{3}{S_{\Delta ABC}}.SH = \frac{1}{3}.\frac{{{a^2}}}{2}.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{{12}}\)
