
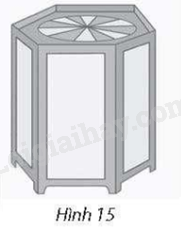
Một hộp đèn treo trần có hình dạng lăng trụ đứng lục giác đều (Hình 15), cạnh đáy bằng 10cm và cạnh bên bằng 50cm. Tính tỉ số giữa diện tích xung quanh và diện tích một mặt đáy của hộp đèn.

Sử dụng kiến thức về diện tích xung quanh hình lăng trụ đứng: Diện tích xung quanh hình lăng trụ đứng bằng chu vi đáy nhân chiều cao.

Diện tích xung quanh của hình lăng trụ đứng là: \({S_{xq}} = 50.6.10 = 3000\left( {c{m^2}} \right)\)
Advertisements (Quảng cáo)
Hình lăng trụ lục giác đứng lục giác đều có đáy là lục giác đều.
Chia lục giác đều thành 6 tam giác đều như hình vẽ:
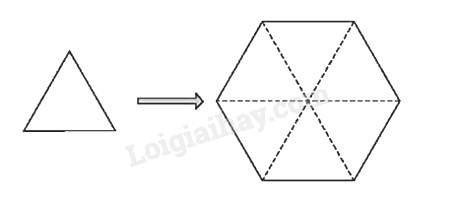
Diện tích một tam giác đều là: \(\frac{{{{10}^2}\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
Diện tích đáy hình lăng trụ đứng lục giác đều là: \({S_{đáy}} = 6.\frac{{{{10}^2}\sqrt 3 }}{4} = 150\sqrt 3 \left( {c{m^2}} \right)\)
Vậy tỉ số giữa diện tích xung quanh và diện tích một mặt đáy của hộp đèn là: \(\frac{{3000}}{{150\sqrt 3 }} = \frac{{20\sqrt 3 }}{3}\)
