
Khẳng định nào sau đây đúng?
A. Hàm số \(y = \cos x\) nghịch biến trên khoảng \(( - \pi ;0)\) và đồng biến trên khoảng \((0;\pi )\).
B. Hàm số \(y = \cos x\) đồng biến trên các khoảng \(( - \pi ;0)\) và \((0;\pi )\).
C. Hàm số \(y = \cos x\) nghịch biến trên các khoảng \(( - \pi ;0)\) và \((0;\pi )\).
D. Hàm số \(y = \cos x\) đồng biến trên khoảng \(( - \pi ;0)\) và nghịch biến trên khoảng \((0;\pi )\).

Advertisements (Quảng cáo)
Dựa vào lý thuyết hàm số \(y = \cos x\) đồng biến trên khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\).
Hoặc dựa vào đồ thị hàm số để khẳng định tính đồng biến nghịch biến của nó.

Đáp án D.
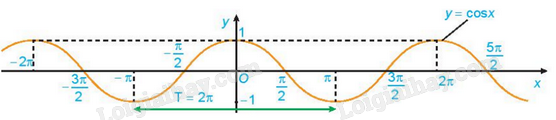
Dựa vào đồ thị, ta thấy hàm số \(y = \cos x\) đồng biến trên khoảng \(( - \pi ;0)\) và nghịch biến trên khoảng \((0;\pi )\).
