
Cho hình lăng trụ \(ABC \cdot A’B’C’\) có \(AA’B’C’\) là hình tứ diền đều cạnh bằng \(a\). Thể tích khối lăng trụ \(ABC \cdot A’B’C’\) bằng
A. \(\frac{{{a^3}\sqrt 2 }}{{12}}\).
B. \(\frac{{{a^3}\sqrt 2 }}{4}\).
C. \(\frac{{{a^3}\sqrt 6 }}{3}\).
D. \(\frac{{{a^3}\sqrt 6 }}{{12}}\).

Gọi \(O\) là tâm đáy\(A’B’C’\),\(O\) là trọng tâm đáy\(A’B’C’\)
Suy \(AO \bot \left( {\;A’B’C’} \right)\)
Tính \(AO,\) diện tích tam giác \(A’B’C’\)
Advertisements (Quảng cáo)
Thể tích khối lăng trụ \(ABC.A’B’C’\) bằng\(V = AO.{S_{A’B’C’}}\)

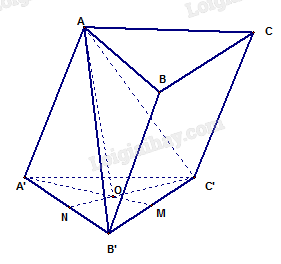
Do tứ diện \(AA’B’C’\) là hình tứ diền đều cạnh bằng \(a\).
Gọi \(O\) là tâm đáy\(A’B’C’\),\(O\) là trọng tâm đáy\(A’B’C’\)
\(A’M = \frac{{a\sqrt 3 }}{2};A’O = \frac{2}{3}A’M = \frac{{a\sqrt 3 }}{3}\)
Ta có \(AO \bot \left( {\;A’B’C’} \right) \Rightarrow AO = \sqrt {A{{A’}^2} - A'{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 6 }}{3}\)
Diện tích tam giác \(A’B’C’:S = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích khối lăng trụ \(ABC \cdot A’B’C’\) bằng\(V = AO.{S_{A’B’C’}} = \frac{{a\sqrt 6 }}{3}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 2 }}{4}\)
Chọn B
