
Cho hình hộp chữ nhật \(ABCD \cdot A’B’C’D’\) có \(AB = AD = a,AA’ = a\sqrt 2 \). Thể tích khối tứ diện \(ACB’D’\) bằng
A. \(\frac{{{a^3}\sqrt 2 }}{3}\).
B. \(\frac{{{a^3}\sqrt 2 }}{6}\).
C. \(\frac{{{a^3}\sqrt 6 }}{3}\).
D. \(\frac{{{a^3}\sqrt 6 }}{6}\).

Phân chia khối hộp chữ nhật thành 5 khối ta có
\({V_{ABCD.A\prime BC\prime D\prime }} = {V_{ACB\prime D\prime }} + {V_{B\prime .ABC}} + {V_{D\prime .ACD}} + {V_{A.A\prime B\prime D\prime }} + {V_{C.B\prime C\prime D\prime }}\)
Chứng minh \(V_{B\prime .ABC}^{} = \frac{1}{6}{V_{ABCD.A\prime BC\prime D\prime }}\)
Chứng minh tương tự ta có: \({V_{D\prime .ACD}} = {V_{A.A\prime B\prime D\prime }} = {V_{C.B\prime C\prime D\prime }} = \frac{1}{6}{V_{ABCD.A\prime BC\prime D\prime }}\)
Suy ra : \({V_{ACB\prime D\prime }} = \frac{1}{3}{V_{ABCD.A\prime BC\prime D\prime }}\)
Advertisements (Quảng cáo)
Tính \({V_{ABCD.A\prime B\prime C\prime D\prime }}\)
Suy ra \({V_{ACB\prime D\prime }} = \frac{1}{3}{V_{ABCD.A\prime B\prime C\prime D\prime }} = \frac{1}{3}{a^3}\sqrt 2 \)

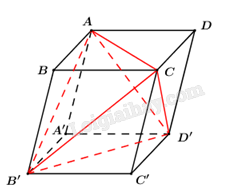
Ta có: \({V_{ABCD.A\prime BC\prime D\prime }} = {V_{ACB\prime D\prime }} + {V_{B\prime .ABC}} + {V_{D\prime .ACD}} + {V_{A.A\prime B\prime D\prime }} + {V_{C.B\prime C\prime D\prime }}\)
Ta có: \(V_{B\prime .ABC}^{} = \frac{1}{3}d(B\prime ;(ABC)).{S_{\Delta ABC}} = \frac{1}{3}d(B\prime ;(ABCD)).\frac{1}{2}{S_{ABCD}} = \frac{1}{6}{V_{ABCD.A\prime BC\prime D\prime }}\)
Chứng minh tương tự ta có: \({V_{D\prime .ACD}} = {V_{A.A\prime B\prime D\prime }} = {V_{C.B\prime C\prime D\prime }} = \frac{1}{6}{V_{ABCD.A\prime BC\prime D\prime }}\)
Khi đó ta có:
\( = {V_{ACB\prime D\prime }} + 4.\frac{1}{6}{V_{ABCD.A\prime BC\prime D\prime }} \Leftrightarrow {V_{ACB\prime D\prime }} = \frac{1}{3}{V_{ABCD.A\prime BC\prime D\prime }}\)
\({V_{ABCD.A\prime B\prime C\prime D\prime }} = AB.AD.AA’ = a.a.a\sqrt 2 = {a^3}\sqrt 2 \)
Vậy \({V_{ACB\prime D\prime }} = \frac{1}{3}{V_{ABCD.A\prime B\prime C\prime D\prime }} = \frac{1}{3}{a^3}\sqrt 2 \)
Chọn A
