
Tìm \(m\) để hàm số sau liên tục trên toàn bộ tập số thực \(\mathbb{R}\):
\(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\frac{{\sqrt {x + 5} - 2}}{{x + 1}}}&{{\rm{\;khi\;}}x > - 1}\\{m \cdot {4^{ - x}} + 1}&{{\rm{\;khi\;}}x \le - 1}\end{array}} \right.\)

Xét tính liên tục của hàm số\(f(x) = \left\{ \begin{array}{l}{f_1}(x)\,khi\,x \ge {x_0}\\{f_2}(x)\,khi\,x
Cách giải :
*Xét tính liên tục của hàm số tại \(x = {x_0}\)
Hàm số \(f\left( x \right)\) liên tục tại \({x_0}\)
*Xét tính liên tục của hàm số với mọi \(x > {x_0}\)
Advertisements (Quảng cáo)
*Xét tính liên tục của hàm số với mọi \(x

Dễ thấy hàm số liên tục trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\).
Hàm số liên tục trên toàn bộ tập số thực \(\mathbb{R}\) khi và chỉ khi hàm số liên tục tại \(x = - 1\).
Ta xét tính liên tục của hàm số tại \(x = - 1\).
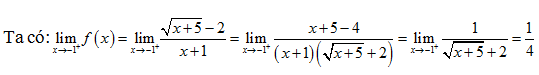
\(\mathop {\lim }\limits_{x \to - {1^ - }} f(x) = \mathop {\lim }\limits_{x \to - {1^ - }} \left( {m{{.4}^{ - x}} + 1} \right) = 4m + 1\) và \(f\left( { - 1} \right) = 4m + 1\)
Suy ra hàm số liên tục trên \(\mathbb{R}\) khi và chỉ khi \(\frac{1}{4} = 4m + 1 \Leftrightarrow m = - \frac{3}{{16}}\).
