
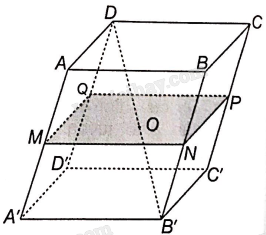
Cho hình hộp ABCD.A’B’C’D’. Gọi O là giao điểm của các đường chéo của hình hộp. Mặt phẳng qua O và song song với mặt phẳng (ABCD) cắt các cạnh AA’, BB’, CC’, DD’ lần lượt tại M, N, P, Q.
a) Chứng minh rằng M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’.
b) Chứng minh rằng ABCD.MNPQ là hình hộp.

Định lý Thalès: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ
Hình lăng trụ tứ giác ABCD.A’B’C’D’ có hai đáy là hình bình hành được gọi là hình hộp.

Advertisements (Quảng cáo)
a) Áp dụng định lý Thalès cho ba mặt phẳng (ABCD), (MNPQ), (A’B’C’D’) và hai cát tuyến AA’, DB’ ta có: \(\frac{{AM}}{{MA’}} = \frac{{DO}}{{OB’}}\)
Vì O là trung điểm của DB’ nên M là trung điểm của AA’.
Chứng minh tương tự ta có: N, P, Q lần lượt là trung điểm của BB’, CC’, DD’.
b) Vì M, N lần lượt là trung điểm của AA’, BB’ nên MN//AB, \(MN = AB\)
Tương tự ta có: PQ//CD và \(PQ = CD\)
Vì \(AB = CD\) và AB//CD nên \(MN = PQ\) và MN//PQ.
Do đó tứ giác MNPQ là hình bình hành.
Vì các đường thẳng AM, BN, CP, DQ đôi một song song nên suy ra ABCD.MNPQ là hình hộp.
