Định lí Thalès trong không gian: Ba mặt phẳng đôi một song song chắn hai cát tuyến phân biệt bất kì những đoạn thẳng tỉ lệ. Hướng dẫn giải - Bài 4.51 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống - Bài tập cuối chương IV. Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C...

Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng d cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C. Đường thẳng d’ cắt các mặt phẳng (P), (Q), (R) lần lượt tại A’, B’, C’. Biết rằng \(\frac{{AB}}{{AC}} = \frac{2}{3}\), tỉ số \(\frac{{A’B’}}{{A’C’}}\) bằng
A. \(\frac{1}{3}\)
B. \(\frac{2}{3}\)
C. \(\frac{3}{2}\)
D. \(\frac{1}{2}\).
Advertisements (Quảng cáo)

Định lý Thalès trong không gian: Ba mặt phẳng đôi một song song chắn hai cát tuyến phân biệt bất kì những đoạn thẳng tỉ lệ.

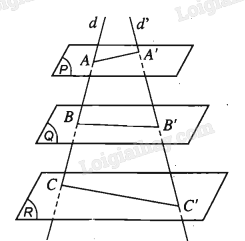
Đáp án B.
Áp dụng định lý Thalès cho ba mặt phẳng đôi một song song (P), (Q), (R) và hai cát tuyến d, d’ ta có: \(\frac{{A’B’}}{{A’C’}} = \frac{{AB}}{{AC}} = \frac{2}{3}\)
