Cho hai hình bình hành ABCD và ABEF không nằm trong một mặt phẳng. M là một điểm của cạnh AD, N là một điểm chuyển động trên cạnh BE sao cho \({{AM} \over {A{\rm{D}}}} = {{BN} \over {BE}}\).
a) Chứng minh rằng MN luôn song song với một mặt phẳng cố định.
b) Tìm tập hợp trung điểm G của đoạn thẳng MN.

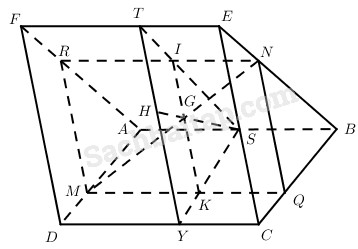
a) Kẻ \(MQ//AB\left( {Q \in BC} \right)\), kẻ \(N{\rm{R}}//AB\left( {R \in AF} \right)\). Dễ thấy tứ giác MQNR là hình bình hành có các cạnh lần lượt song song với AB và EC. Từ đó suy ra MN luôn song song với mặt phẳng cố định (CDFE).
Advertisements (Quảng cáo)
b) Gọi S, T, Y lần lượt là trung điểm AB, EF, CD; I, K lần lượt là trung điểm của NR và QM. Khi đó, dễ thấy G là trung điểm của IK và I, K lần lượt là giao điểm của các cặp đường thẳng NR và ST, MQ và SY.
Gọi H là trung điểm của TY, thì rõ ràng S, G, H thẳng hàng và SH là đường trung tuyến của tam giác cố định STY. Vậy tập hợp các điểm G là đường trung tuyến SH của tam giác STY.
Phần đảo. Lấy một điểm G bất kì trên đoạn thẳng SH, qua G kẻ đường thẳng \(IK//TY\left( {I \in ST,K \in SY} \right)\). Qua I và K kẻ lần lượt các đường thẳng NR và MQ cùng song song với AB (N ∈ EB, R ∈ AF, M ∈ AD, Q ∈ BC).
Sau đó chứng minh G là trung điểm của MN và \({{AM} \over {A{\rm{D}}}} = {{BN} \over {BE}}\).
