Cho hình bình hành ABCD. Qua đỉnh A, B, C, D dựng các đường thẳng a, b, c, d tương ứng song song với nhau và không thuộc mp(ABCD). Trên mỗi đường thẳng a, b, c, d lần lượt lấy các điểm \({A_1},{B_1},{C_1},{D_1}\). Chứng minh rằng:
a) Nếu các điểm \({A_1},{B_1},{C_1},{D_1}\) không đồng phẳng thì đường thẳng nối trung điểm A1C1 và trung điểm B1D1 luôn đi qua một điểm cố định.
b) Bốn điểm \({A_1},{B_1},{C_1},{D_1}\) đồng phẳng khi và chỉ khi trung điểm của A1C1 trùng với trung điểm B1D1.
c) Nếu bốn đường thẳng \(A{C_1},B{{\rm{D}}_1},C{A_1},D{B_1}\) đôi một cắt nhau thì \(ABC{\rm{D}}.{A_1}{B_1}{C_1}{D_1}\) là một hình hộp.

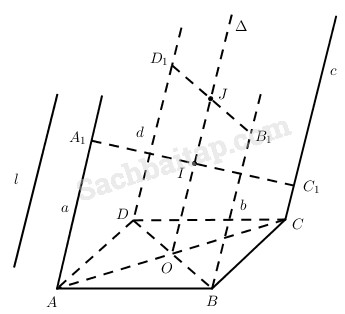
a) Xét phép chiếu song song lên mp(ABCD) theo phương chiếu l // a. Khi đó A1C1 có hình chiếu là AC nên trung điểm I của A1C1 có hình chiếu là trung điểm O của AC.
Tương tự, trung điểm J của B1D1 có hình chiếu là trung điểm O của BD.
Do đó, ba điểm I, J, O phải nằm trên một đường thẳng ∆. Đường thẳng ∆ này đi qua điểm cố định O.
b) Nếu \({A_1},{B_1},{C_1},{D_1}\) đồng phẳng thì \({A_1}{B_1}//{C_1}{D_1}\) vì chúng là giao tuyến của \(mp\left( {{A_1}{B_1}{C_1}{D_1}} \right)\) với hai mặt phẳng song song \(\left( {AB{B_1}{A_1}} \right),\left( {DC{C_1}{D_1}} \right)\).
Tương tự, ta có \({A_1}{D_1}//{B_1}{C_1}\). Vậy tứ giác \({A_1}{B_1}{C_1}{D_1}\) là một hình bình hành. Do đó trung điểm I của A1C1 trùng với trung điểm J của B1D1.
Advertisements (Quảng cáo)
● Ngược lại, nếu I trùng với J thì các điểm \({A_1},{B_1},{C_1},{D_1}\) cùng nằm trên mặt phẳng xác định bởi hai đường thẳng cắt nhau A1C1 và B1D1.
c)
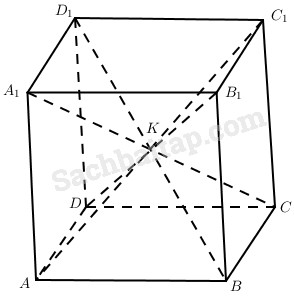
Giả sử AC1 cắt BD1 tại K. Khi đó, ta có \(mp\left( {A{C_1},B{{\rm{D}}_1}} \right) \equiv mp\left( {AB{C_1}{D_1}} \right)\).
Mặt phẳng này cắt hai mặt phẳng song song \(\left( {AB{B_1}{A_1}} \right),\left( {DC{C_1}{D_1}} \right)\) theo hai giao tuyến song song AB và C1D1, suy ra \({C_1}{D_1}//C{\rm{D}}\). Mặt khác \(D{D_1}//C{C_1}\).
Vậy tứ giác \(CD{D_1}{C_1}\) là hình bình hành.
Do đó: \(C{\rm{D}} = {C_1}{D_1} \Rightarrow {C_1}{D_1} = BA\).
Như vậy \(AB{C_1}{D_1}\) là hình bình hành và K là trung điểm của AC1 và BD1.
Tương tự, nếu BD1 cắt CA1 tại K’ thì \(BC{{\rm{D}}_1}{A_1}\) là hình bình hành và K’ là trung điểm của BD1 và CA1 nên K’ ≡ K.
Tương tự, ta cũng suy ra K là trung điểm của B1D, các mặt \(AB{B_1}{A_1},BC{C_1}{B_1}\) đều là hình bình hành và từ đó \({A_1}{B_1}{C_1}{D_1}\) cũng là hình bình hành. Vậy \(ABC{\rm{D}}.{A_1}{B_1}{C_1}{D_1}\) là hình hộp.
