Cho hình chữ nhật ABCD có AB = a, BC = b. Xét hai tia At, Ct’ cùng chiều và cùng vuông góc với mp(ABC). Lấy điểm M thuộc At, N thuộc Ct’ (M ≠ A, N ≠ C). Đặt AM = m, CN = n.
a) Tính góc giữa các mặt phẳng (MBD) và (NBD) với mặt phẳng (ABCD).
b) Tính góc giữa hai mặt phẳng (MBD) và (NBD). Tìm hệ thức giữa a, b, m, n để hai mặt phẳng đó vuông góc.
c) Khi a = b và mp(MBD) vuông góc với mp(NBD), hãy tính đường cao OI của tam giác MON (trong đó O là giao điểm của AC và BD), từ đó suy ra hai mặt phẳng (BMN) và (DMN) vuông góc với nhau.

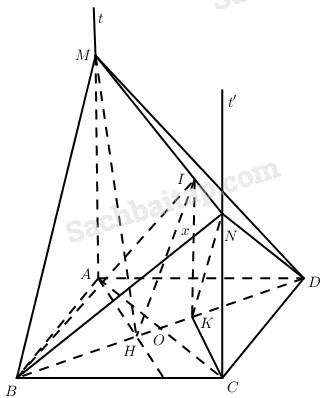
a) Kẻ \(AH \bot B{\rm{D}}\). Do \(MA \bot \left( {ABC{\rm{D}}} \right)\) nên \(MH \bot B{\rm{D}}\) (định lí ba dường vuông góc).
Ta có MAH là tam giác vuông tại A nên \(\widehat {MHA}\) là góc giữa mp(MBD) với mp(ABCD). Đặt \(\widehat {MHA} = \alpha \) thì
\(\eqalign{ & \tan \alpha = {{MA} \over {AH}},MA = m \cr & AH = {{ab} \over {\sqrt {{a^2} + {b^2}} }} \cr & \Rightarrow \tan \alpha = {{m\sqrt {{a^2} + {b^2}} } \over {ab}} \cr} \)
Vậy góc giữa mặt phẳng (MBD) và mặt phẳng (ABCD) là α mà
\(\tan \alpha = {{m\sqrt {{a^2} + {b^2}} } \over {ab}}\)
Tương tự, ta có \(\widehat {NKC}\) là góc giữa mp(NBD) với mp(ABCD) và đặt \(\widehat {NKC} = \beta \) thì
\(\tan \beta = {{n\sqrt {{a^2} + {b^2}} } \over {ab}}\)
Vậy góc giữa mặt phẳng (NBD) và mặt phẳng (ABCD) là β mà
\(\tan \beta = {{n\sqrt {{a^2} + {b^2}} } \over {ab}}\)
b) Kẻ Hx song song với KN, do AH // KC và At, Ct’ nằm về một phía của (ABCD) nên \(\widehat {MH{\rm{x}}}\) hoặc \({180^0} - \widehat {MH{\rm{x}}}\) là góc giữa hai mặt phẳng (MBD) và (NBD).
Đặt \(\widehat {MH{\rm{x}}} = \gamma \) thì \(\gamma = {180^0} - \left( {\alpha + \beta } \right)\)
Advertisements (Quảng cáo)
\(\eqalign{ & \tan \gamma = - tan\left( {\alpha + \beta } \right) = {{\tan \alpha + \tan \beta } \over {\tan \alpha \tan \beta - 1}} \cr & = {{\sqrt {{a^2} + {b^2}} \left( {m + n} \right)ab} \over {mn\left( {{a^2} + {b^2}} \right) - {a^2}{b^2}}} \cr} \)
Vậy góc giữa hai mặt phẳng (MBD) và (NBD) là φ mà
\(\tan \varphi = {{\sqrt {{a^2} + {b^2}} \left( {m + n} \right)ab} \over {\left| {mn\left( {{a^2} + {b^2}} \right) - {a^2}{b^2}} \right|}}\)
Từ đó, suy ra mặt phẳng (MBD) và mặt phẳng (NBD) vuông góc khi và chỉ khi
\(mn\left( {{a^2} + {b^2}} \right) - {a^2}{b^2} = 0\) hay \(mn = {{{a^2}{b^2}} \over {{a^2} + {b^2}}}\).
c)
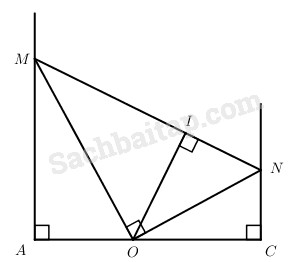
Khi a = b thì H ≡ K ≡ O và \(mp\left( {MB{\rm{D}}} \right) \bot mp\left( {NB{\rm{D}}} \right)\) tức là \(mn = {{{a^2}} \over 2}\).
Gọi OI là đường cao của tam giác vuông OMN.
Ta có
\(\eqalign{ & OI = {{2{{\rm{S}}_{MON}}} \over {MN}} \cr & 2{{\rm{S}}_{MON}} = 2\left[ {{S_{ACNM}} - \left( {{S_{AM{\rm{O}}}} + {S_{CNO}}} \right)} \right] \cr & = 2\left( {{1 \over 2}\left( {m + n} \right)a\sqrt 2 - {1 \over 2}.{{a\sqrt 2 } \over 2}m - {1 \over 2}.{{a\sqrt 2 } \over 2}n} \right) \cr & = {{a\sqrt 2 } \over 2}\left( {m + n} \right) \cr & MN = \sqrt {{{\left( {m - n} \right)}^2} + 2{{\rm{a}}^2}} \cr & = \sqrt {{{\left( {m - n} \right)}^2} + 4mn} \cr & = m + n \cr} \)
Từ đó \(OI = {{a\sqrt 2 } \over 2}\)
Vậy BID là tam giác vuông tại I.
Mặt khác \(B{\rm{D}} \bot \left( {MACN} \right)\) nên \(B{\rm{D}} \bot MN\) ; kết hợp với \(OI \bot MN\) ta có \(MN \bot \left( {BI{\rm{D}}} \right)\).
Vì \(\widehat {BI{\rm{D}}} = {90^0}\) nên hai mặt phẳng (BMN) và (DMN) vuông góc với nhau.
