Tìm giao tuyến của hai mặt phẳng (DBC) và (DMN).. Bài 2.11 trang 70 Sách bài tập (SBT) Hình học 11 - Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
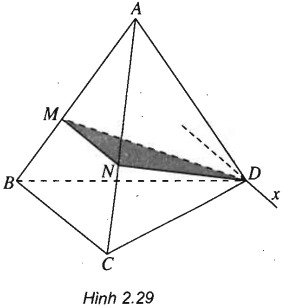
Cho tứ diện ABCD. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao cho . Tìm giao tuyến của hai mặt phẳng (DBC) và (DMN).
(h.2.29)
\(\left\{ \matrix{
M \in AB \hfill \cr
N \in AC \hfill \cr} \right. \Rightarrow MN \subset \left( {ABC} \right)\)
Advertisements (Quảng cáo)
Trong tam giác ABC ta có:
\({{AM} \over {AB}} = {{AN} \over {AC}} \Rightarrow MN\parallel BC\)
Hiển nhiên \(D \in \left( {DBC} \right) \cap \left( {DMN} \right)\)
\(\left\{ \matrix{
BC \subset \left( {DBC} \right) \hfill \cr
MN \subset \left( {DMN} \right) \hfill \cr
BC\parallel MN \hfill \cr} \right.\)
\( \Rightarrow \left( {DBC} \right) \cap \left( {DMN} \right) = Dx\) và \(Dx\parallel BC\parallel MN\)