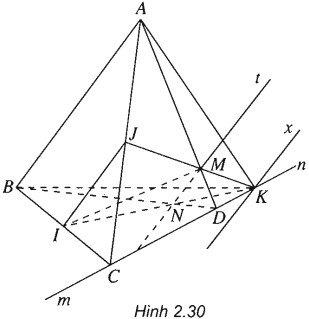
Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC , M là một điểm tùy ý trên cạnh AD.
a) Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD)
b) Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và IM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không là trung điểm của AD).
c) Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ).

(h.2.30)
a)
\(\left\{ \matrix{
M \in \left( {MIJ} \right) \hfill \cr
M \in AD \Rightarrow M \in \left( {ABD} \right) \hfill \cr} \right. \Rightarrow M \in \left( {MIJ} \right) \cap \left( {ABD} \right)\)
Ta cũng có:
\(\left\{ \matrix{
IJ\parallel AB \hfill \cr
IJ \subset \left( {MIJ} \right) \hfill \cr
AB \subset \left( {ABD} \right) \hfill \cr} \right.\)
Advertisements (Quảng cáo)
\( \Rightarrow \left( {MIJ} \right) \cap \left( {ABD} \right) = d = Mt\) và \(Mt\parallel AB\parallel IJ\)
b) Ta có: \(Mt\parallel AB \Rightarrow Mt \cap BD = N\)
\(IN \cap JM = K \Rightarrow \left\{ \matrix{
K \in IN \hfill \cr
K \in JM \hfill \cr} \right.\)
Vì \(K \in IN \Rightarrow K \in \left( {BC{\rm{D}}} \right)\)
Và \(K \in JM \Rightarrow K \in \left( {AC{\rm{D}}} \right)\)
Mặt khác \(\left( {BC{\rm{D}}} \right) \cap \left( {AC{\rm{D}}} \right) = C{\rm{D}}\) do đó \(K \in C{\rm{D}}\). Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD. ( Để ý rằng nếu M là trung điểm của AD thì sẽ không có điểm K.)
c) Ta có:
\(\left\{ \matrix{
K \in \left( {ABK} \right) \hfill \cr
K \in IN \Rightarrow K \in \left( {MIJ} \right) \hfill \cr} \right. \Rightarrow K \in \left( {ABK} \right) \cap \left( {MIJ} \right)\)
Mà
\(\left\{ \matrix{
AB \subset \left( {ABK} \right) \hfill \cr
IJ \subset \left( {MIJ} \right) \hfill \cr
AB\parallel IJ \hfill \cr} \right. \Rightarrow \left( {ABK} \right) \cap \left( {MIJ} \right) = Kx\) và \(K{\rm{x}}\parallel AB\parallel IJ\)
