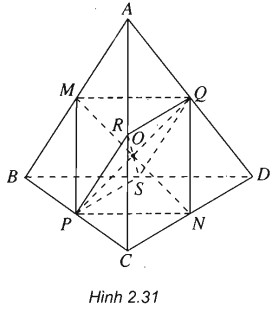
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.

(h.2.31)
Trong tam giác ABC ta có:
\(MP\parallel AC\) và \(MP = {{AC} \over 2}\).
Trong tam giác ACD ta có:
Advertisements (Quảng cáo)
\(QN\parallel AC\) và \(QN = {{AC} \over 2}\).
Từ đó suy ra \(\left\{ \matrix{MP\parallel QN \hfill \crMP = QN \hfill \cr} \right.\)
⟹ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: \(P{\rm{R}}\parallel Q{\rm{S}}\) và \(P{\rm{R}} = QS = {{AB} \over 2}\). Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
