Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Bài 2.14 trang 71 Sách bài tập (SBT) Hình học 11 - Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng .

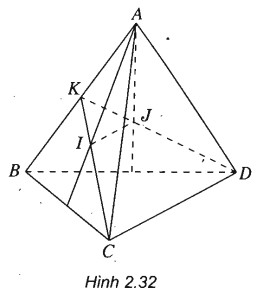
(h.2.32)
Advertisements (Quảng cáo)
Gọi K là trung điểm của AB.
Vì I là trọng tâm của tam giác ABC nên \(I \in KC\) và vì J là trọng tâm của tam giác ABD nên \(J \in KD\).
Từ đó suy ra \({{KI} \over {KC}} = {{KJ} \over {K{\rm{D}}}} = {1 \over 3} \Rightarrow IJ\parallel CD\).
