Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’. Chứng minh
a) \(\left( {A{\rm{D}}F} \right)\parallel \left( {BCE} \right)\).
b) \(M’N’\parallel DF\).
c) \(\left( {DEF} \right)\parallel \left( {MM’N’N} \right)\) và \(MN\parallel \left( {DEF} \right)\).

a)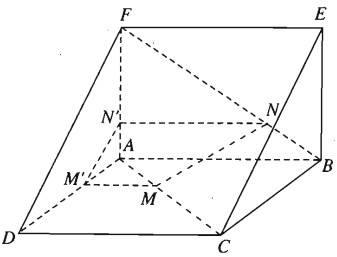
\(\left\{ \matrix{
AD\parallel BC \hfill \cr
BC \subset \left( {BCE} \right) \hfill \cr} \right. \Rightarrow AD\parallel \left( {BCE} \right)\)
\(\left\{ \matrix{
AF\parallel BE \hfill \cr
BE \subset \left( {BCE} \right) \hfill \cr} \right. \Rightarrow AF\parallel \left( {BCE} \right)\)
Mà \(AD,AF \subset \left( {ADF} \right)\)
Advertisements (Quảng cáo)
Nên \(\left( {ADF} \right)\parallel \left( {BCE} \right)\)
b) Vì ABCD và ABEF là các hình vuông nên AC = BF. Ta có:
\(MM’\parallel C{\rm{D}} \Rightarrow {{AM’} \over {A{\rm{D}}}} = {{AM} \over {AC}}\,\,\,\,\,\,\,\left( 1 \right)\)
\(NN’\parallel AB \Rightarrow {{AN’} \over {AF}} = {{BN} \over {BF}}\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
So sánh (1) và (2) ta được \({{AM’} \over {A{\rm{D}}}} = {{AN’} \over {AF}} \Rightarrow M’N’\parallel DF\)
c) Từ chứng minh trên suy ra \(DF\parallel \left( {MM’N’N} \right)\)
\(\left. \matrix{
NN’\parallel AB \Rightarrow NN’\parallel EF \hfill \cr
NN’ \subset \left( {MM’N’N} \right) \hfill \cr} \right\} \Rightarrow EF\parallel \left( {MM’N’N} \right)\)
Mà \(DF,EF \subset \left( {DEF} \right)\) nên \(\left( {DEF} \right)\parallel \left( {MM’N’N} \right)\)
Vì \(MN \subset \left( {MM’N’N} \right)\) và \(\left( {MM’N’N} \right)\parallel \left( {DEF} \right)\) nên \(MN\parallel \left( {DEF} \right)\).
