Advertisements (Quảng cáo)
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của A’B’.
a) Chứng minh rằng \(CB’\parallel \left( {AHC’} \right)\)
b) Tìm giao tuyến d của (AB’C’) và (ABC)
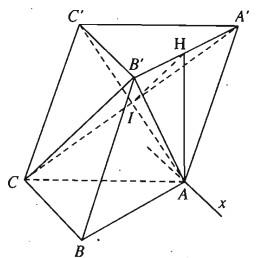
a) Ta có tứ giác AA’CC’ là hình bình hành suy ra A’C cắt AC’ tại trung điểm I của mỗi đường.
Do đó \(IH\parallel CB’\) ( đường trung bình của tam giác CB’A’)
Mặt khác \(IH \subset \left( {AHC’} \right)\) nên \(CB’\parallel \left( {AHC’} \right)\)
b) Ta có:
\(\left\{ \matrix{
A \in \left( {AB’C’} \right) \hfill \cr
A \in \left( {ABC} \right) \hfill \cr} \right.\)
⇒ A là điểm chung của (AB’C’) và (ABC)
Mà
\(\left\{ \matrix{
B’C’\parallel BC \hfill \cr
B’C’ \subset \left( {AB’C’} \right) \hfill \cr
BC \subset \left( {ABC} \right) \hfill \cr} \right.\)
Nên \(\left( {AB’C’} \right) \cap \left( {ABC} \right) = Ax\)
Và \(Ax\parallel BC\parallel B’C’\)