Cho hai hình bình hành ABCD và ABEF không nằm cùng trong một mặt phẳng. Gọi M và N là hai điểm di động tương ứng trên AD và BE sao cho . Bài 2.27 trang 80 Sách bài tập (SBT) Hình học 11 - Bài 4. Hai mặt phẳng song song
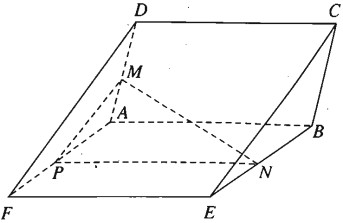
Cho hai hình bình hành ABCD và ABEF không nằm cùng trong một mặt phẳng. Gọi M và N là hai điểm di động tương ứng trên AD và BE sao cho
\({{AM} \over {M{\rm{D}}}} = {{BN} \over {NE}}\)
Chứng minh rằng đường thẳng MN luôn luôn song song với một mặt phẳng cố định. Hãy chỉ ra mặt phẳng cố định đó.
Advertisements (Quảng cáo)
Trong mặt phẳng (ADF), kẻ đường thẳng \(MP\parallel DF\left( {P \in AF} \right)\)
Ta có \({{AP} \over {PF}} = {{AM} \over {M{\rm{D}}}} = {{BN} \over {NE}}\)
Nên \(PN\parallel F{\rm{E}}\). Do đó \(\left( {MNP} \right)\parallel \left( {DEF} \right)\).
Vậy MN song song với mặt phẳng (DEF) cố định.