Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Bài 3.19 trang 147 Sách bài tập (SBT) Hình học 11 - Bài 3. Đường thẳng vuông góc với mặt phẳng
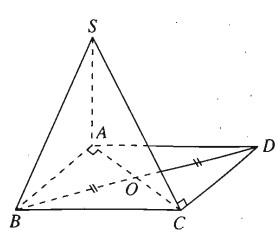
Hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A và có cạnh bên SA vuông góc với mặt phẳng đáy là (ABC). Gọi D là điểm đối xứng của của điểm B qua trung điểm O của cạnh AC. Chứng minh rằng \(C{\rm{D}} \bot CA\) và \(C{\rm{D}} \bot \left( {SCA} \right)\).
Advertisements (Quảng cáo)
Ta có
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot DC \subset \left( {ABC} \right)\)
Vì AC và BD cắt nhau tại trung điểm Ocủa mỗi đoạn nên tứ giác ABCD là hình bình hành và ta có \(AB\parallel C{\rm{D}}\). Vì \(AB \bot AC\) nên \(C{\rm{D}} \bot CA\). Mặt khác ta có \(C{\rm{D}} \bot SA\), do đó \(C{\rm{D}} \bot \left( {SCA} \right)\)