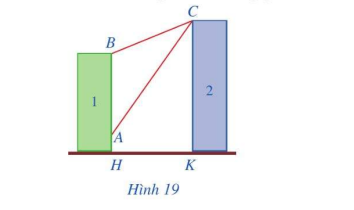
Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là \(HK = 20m\). Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 19). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là \(CK = 32m,AH = 6m,BH = 24m\) (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
Dựa vào công thức cộng để tính
Từ C kẻ CD vuông góc với AB
Ta có: \(AD = CK - AH = 32 - 6 = 26\left( m \right)\)
\(\begin{array}{l}AB = BH - AH = 24 - 6 = 18\left( m \right)\\DB = AD - AB = 26 - 18 = 8\left( m \right)\end{array}\)
\(CD = HK = 20m\)
Ta có: \(\tan DCB = \frac{{DB}}{{CD}} = \frac{8}{{20}} = \frac{2}{5}\)
\(\tan DCA = \frac{{DA}}{{DC}} = \frac{{26}}{{20}} = \frac{{13}}{{10}}\)
\[\begin{array}{l}\tan BCA = \tan \left( {DCA - DCB} \right) = \frac{{\tan DCA - \tan DCB}}{{1 + \tan DCA.\tan DCB}} = \frac{{\frac{{13}}{{10}} - \frac{2}{5}}}{{1 + \frac{{13}}{{10}}.\frac{2}{5}}} = \frac{{45}}{{76}}\\ \Rightarrow \widehat {ACB} \approx 30,6^\circ \end{array}\]