. Giải và trình bày phương pháp giải lý thuyết Hàm số lượng giác và đồ thị - SGK Toán 11 Cánh Diều Bài 3. Hàm số lượng giác và đồ thị. I. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn...
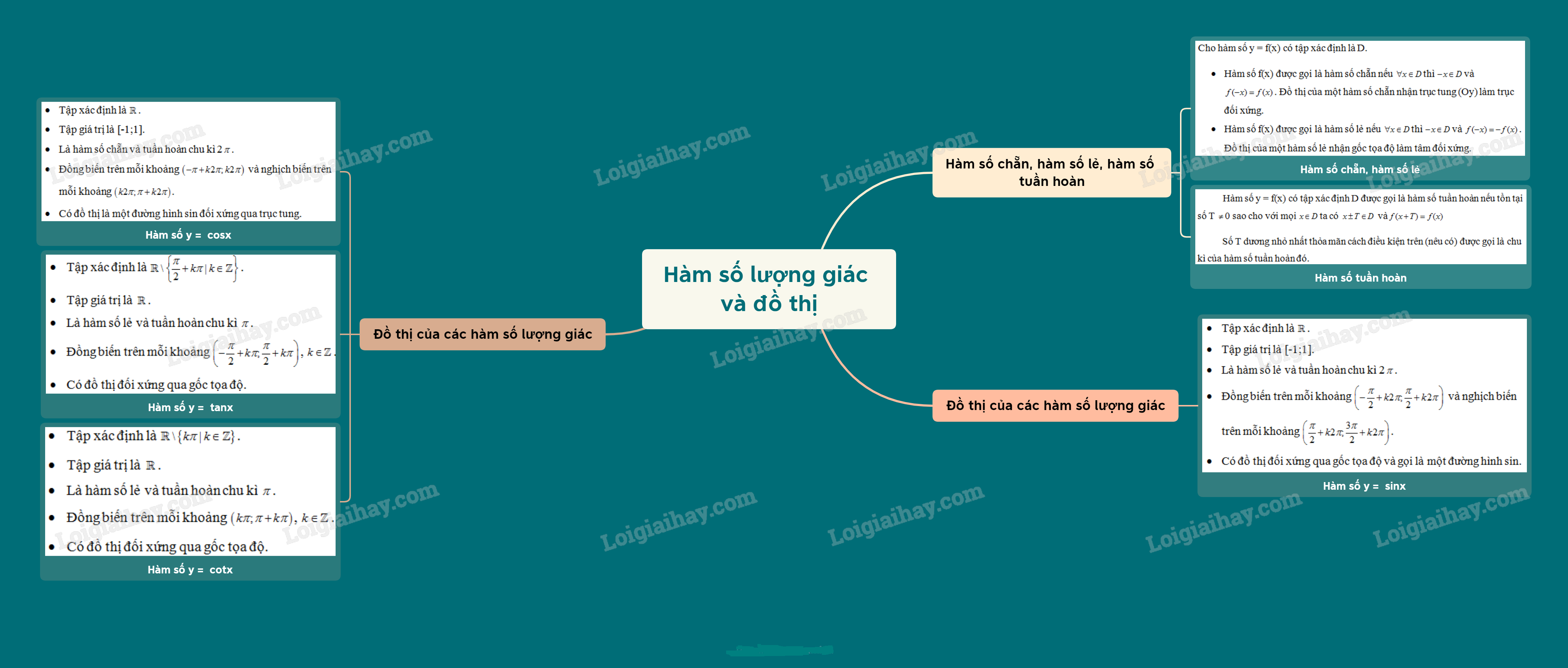
I. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
1. Hàm số chẵn, hàm số lẻ
Cho hàm số y = f(x) có tập xác định là D.
- Hàm số f(x) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = f(x)\). Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.
- Hàm số f(x) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = - f(x)\). Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
2. Hàm số tuần hoàn
Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T \( \ne \) 0 sao cho với mọi \(x \in D\) ta có:
- \(x + T \in D\) và \(x - T \in D\)
- \(f(x + T) = f(x)\)
Advertisements (Quảng cáo)
Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.
3. Đồ thị và tính chất của hàm số y = sinx
- Tập xác định là \(\mathbb{R}\).
- Tập giá trị là [-1;1].
- Là hàm số lẻ và tuần hoàn chu kì 2\(\pi \).
- Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\).
- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
4. Đồ thị và tính chất của hàm số y = cosx
- Tập xác định là \(\mathbb{R}\).
- Tập giá trị là [-1;1].
- Là hàm số chẵn và tuần hoàn chu kì 2\(\pi \).
- Đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\).
- Có đồ thị là một đường hình sin đối xứng qua trục tung.
5. Đồ thị và tính chất của hàm số y = tanx
- Tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
- Tập giá trị là \(\mathbb{R}\).
- Là hàm số lẻ và tuần hoàn chu kì \(\pi \).
- Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\), \(k \in \mathbb{Z}\).
- Có đồ thị đối xứng qua gốc tọa độ.
6. Đồ thị và tính chất của hàm số y = cotx
- Tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
- Tập giá trị là \(\mathbb{R}\).
- Là hàm số lẻ và tuần hoàn chu kì \(\pi \).
- Đồng biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\), \(k \in \mathbb{Z}\).
- Có đồ thị đối xứng qua gốc tọa độ.